偽內切圓
幾何學中,三角形的偽內切圓[1]是內切於三角形兩條邊和其外接圓的一個圓。與頂點的兩條邊相切的偽內切圓稱為「關於點的偽內切圓」、「所對的偽內切圓」或「-偽內切圓」。
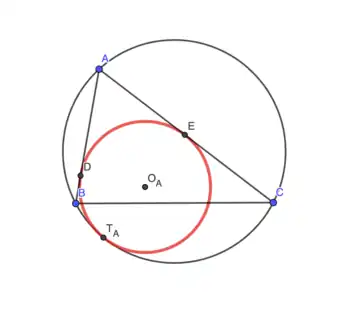
三角形內關於頂點的偽內切圓
關於三角形的每個頂點都有唯一的偽內切圓。
存在性及唯一性的證明
關於點的旁切圓是唯一的。
定義為以下兩個幾何變換的複合:先以點為圓心,為半徑作反演變換;再關於角的平分線作對稱變換。由於反演變換和對稱變換都為雙射且變換前後保留交點的性質,也有對應的性質。
點的旁切圓經變換後的圖像為內切於、,以及外接圓的一個圓,即關於點的偽內切圓。因此關於點的偽內切圓唯一確定。類似地,關於點及點的偽切圓也唯一確定。[2]
其他性質
參考資料
- 潘成华; 田开斌; 褚小光. . 中等数学. 2017, (4): 2–6. ISSN 1005-6416.
与三角形外接圆内切且与三角形的两边相切的圆称为伪内切圆
- Baca, Jafet. (PDF). Mathematical Reflections. 2020, (2) [2023-01-21]. (原始内容存档 (PDF)于2022-10-23).
- Yui, Paul. . The American Mathematical Monthly. 2018-04-23, 106 (10): 952–955 [2021-10-27]. doi:10.1080/00029890.1999.12005146. (原始内容存档于2022-10-23).
- Chen, Evan. . United States of America: MAA. 2016: 68–69. ISBN 978-1-61444-411-4.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.