协方差
协方差矩阵
协方差的定義可以推廣到兩列隨機變數之間
以上的定義,以矩形來表示就是:
相關係數
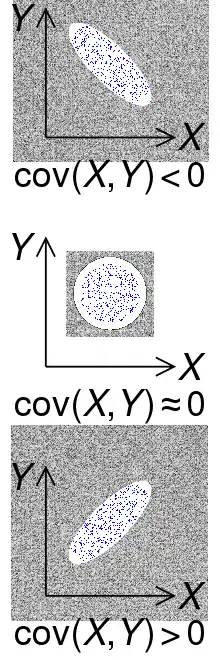
取决于协方差的相关性
更准确地说是线性相关性,是一个衡量线性独立的无量纲数,其取值在之间。相关性时称为“完全线性相关”(相关性时称为“完全线性负相关”),此时将对作Y-X 散点图,将得到一组精确排列在直线上的点;相关性数值介于-1到1之间时,其绝对值越接近1表明线性相关性越好,作散点图得到的点的排布越接近一条直线。
相关性为0(因而协方差也为0)的两个随机变量又被称为是不相关的,或者更准确地说叫作“线性无关”、“线性不相关”,这仅仅表明与两随机变量之间没有线性相关性,并非表示它们之间一定没有任何内在的(非线性)函数关系,和前面所说的“、二者并不一定是统计独立的”说法一致。
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.