凯泽窗
凯泽窗(Kaiser window)是由贝尔实验室的James Kaiser所提出的。凯泽窗是一個單參數的窗函数群,用在数字信号处理中,其定義如下[1][2]:
凯泽窗
其中:
- N 為序列的長度
- I0 是零階的第一類修正貝索函數
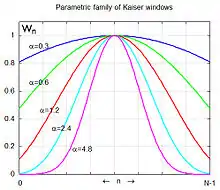
- α 是任意非負實數,用來調整凯泽窗的外形。在頻域上可以在主瓣(main-lobe)寬度及旁瓣(side lobe)大小中取拾,這是窗函數設計的重要考量因素。
若N為奇數,窗函數最大值會在 。若N為偶數,窗函數最大值會在 。
傅立葉變換
若將上述離散數列視為是連續函數,並進行傅立葉變換:

兩個不同α參數凯泽窗的傅立葉變換
w0(t)的最大值為w0(0) = 1. 上述的w[n]數列為以下函收的取様:
- ,在間隔T的時間進行取樣。
而且rect()為矩形函数. W0(f)主瓣後的第一個零點在:
調整α可以在主瓣的寬度及旁瓣大小中進行取捨。若α增加,W0(f)主瓣的寬度增加,而旁瓣的大小減小,如右圖所示。α = 0會對應長方形的窗函數。若α增加,時域及頻率下凯泽窗的形狀都會接近高斯曲線。凯泽窗在頻率0附近的集中程度是幾乎最佳化的(Oppenheim et al., 1999)。
腳註
- Harris, Fredric j. (PDF). Proceedings of the IEEE. Jan 1978, 66 (1): 73–74 [2017-01-29]. doi:10.1109/PROC.1978.10837. (原始内容存档 (PDF)于2017-03-19). Article on FFT windows which introduced many of the key metrics used to compare windows.
- Kaiser, James F.; Ronald W. Schafer. . IEEE Transactions on Acoustics, Speech and Signal Processing. February 1980,. ASSP-28 (1): 105–107.
- Kaiser, James F.; Schafer, Ronald W. . IEEE Transactions on Acoustics, Speech, and Signal Processing. 1980, 28: 105–107. doi:10.1109/TASSP.1980.1163349.
參考資料
- Oppenheim, A. V.; Schafer, R. W.; Buck J. R. . Upper Saddle River, N.J.: Prentice Hall. 1999. ISBN 0-13-754920-2.
- Kaiser, J. F. (1966). Digital Filters. In Kuo, F. F. and Kaiser, J. F. (Eds.), System Analysis by Digital Computer, chap. 7. New York, Wiley.
- Craig Sapp, Kaiser-Bessel Derived Window Examples and C-language Implementation, Music 422 / EE 367C: Perceptual Audio Coding (Stanford University course page, 2001).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.