切比雪夫函數
在數學上,切比雪夫函數(Chebyshev Function)可指一個標量化函數(切比雪夫加權標量化函數),或兩個彼此相關的函數的其中之一。
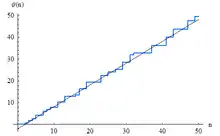
切比雪夫第一函數(First Chebyshev Function)在文獻中一般記做或,其形式如下:
其中是自然對數,而切比雪夫第一函數就是所有小於等於x的質數p的自然對數的總和。
切比雪夫第二函數(Second Chebyshev Function)在文獻中一般記做,其定義類似,為所有小於等於x的質數p的冪的自然對數的總和,而其形式如下:
其中是馮·曼戈爾特函數。切比雪夫函數,尤其切比雪夫第二函數,經常出現於與質數相關的數學證明中,而這是因為這些函數比質數計數函數還容易處理之故。可見下等式一節說明。
切比雪夫第一及第二函數都與x呈現非病態關係,而這點等價於質數定理。
除了上述的切比雪夫第一及第二函數外,還有個與上述無關無關的切比雪夫加權標量化函數(Tchebycheff function或weighted Tchebycheff scalarizing function)或切比雪夫效用函數(Chebyshev utility function),其形式如下:
藉由最小化這方程式不同的數值,可得到帕累托前沿的每個點,甚至是非凸性的部分。[1]很多時候,要最小化的不是,而是在給定標量的狀況下的數值,而在這種狀況下有。[2]
這三個函數皆以帕夫努季·利沃维奇·切比雪夫為名,唯本文的主題是數論上的切比雪夫第一及第二函數,切比雪夫加權標量化函數與這兩函數無關,也不會出現在接下來的討論中。
切比雪夫第一及第二函數的關係
切比雪夫第一及第二函數彼此相關,要驗證這點,可先將切比雪夫第二函數寫成如下形式:
其中k是使得的唯一整數,而k的值可參見A206722。一個更直接的關係如下:
注意的是和的後半段只有有限多個非零數值,而這是因為有下式之故:
切比雪夫第二函數是從1到n所有數的最小公倍數的自然對數:
對於n而言,lcm(1, 2, ..., n)的值可參見A003418。
以下pp定理]]將及這兩個分數給聯繫起來。[3]
定理:若則有
注意:從此不等式可推出
換句話說,若或其中一個趨近某個極限,則另一個也是如此,也就是兩者的極限相等。
證明:由於,因此有
而由的定義,可得以下明顯的不等式:
因此有
最後,將此不等式兩邊除以,即可得定理的不等式。
非病態關係及上下界
對於切比雪夫函數,有以下已知的界線。其中pk是第k個質數,也就是p1 = 2、p2 = 3等等:
此外,若黎曼猜想成立,則對於任意的而言,有以下關係式:
對任意的而言,切比雪夫第一函數及第二函數有以下的上界:[4]
對於1.03883這常數的解釋,可見A206431的說明。
等式
1895年,漢斯·馮·曼戈爾特證明了有以下作為黎曼ζ函數非平凡零點和的解析解:
其中ζ′ (0)/ζ (0)的數值為log(2π)、ρ遍歷黎曼ζ函數的所有非平凡零點,而ψ0是一個與ψ類似的函數,但差別是其在跳躍不連續點(質數的冪)的取值為其左邊與右邊值的中間:
就自然對數的泰勒展開式而言,解析解的最後一項可理解為xω/ω對黎曼ζ函數平凡零點ω = −2, −4, −6, ...的求和。也就是說,
類似地,此公式第一項x = x1/1對應到黎曼ζ函數在1的單純極點。這部分作為極點而非零點的事實,說明了項的變號。
性質
一個由埃哈德·施密特證明的結果指稱,對於某個特定的正常數K,存在有無限多個正整數x使得
同時有無限多個正整數x使得
使用小o符號,可將上式重述為
也就是說有無限多的正整數x,使得與x之間的差的絕對值超過。
與質數階乘的關係
切比雪夫第一函數也是x的質數階乘x #的對數:
這說明了質數階乘x #非病態地等於e(1 + o(1))x,其中o是小o符號(見大O符號一文的說明),而這點與質數定理共同確立了pn #的非病態行為。
與質數計數函數間的關係
切比雪夫函數可透過下式與與質數計數函數發生關係。定義
那麼有
從Π到質數計數函數π間的轉換可由下式表示:
由於很明顯地,有π (x) ≤ x之故,因此為了估計的目的,最後的關係式可重述如下:
平滑化函數
平滑化切比雪夫函數定義如下:
顯然有
參考資料
- Joshua Knowles. (PDF). The University of Manchester: 34. 2 May 2014.
- Ho-Huu, V.; Hartjes, S.; Visser, H. G.; Curran, R. (PDF). Expert Systems with Applications (Delft University of Technology). 2018. Page 6 equation (2). doi:10.1016/j.eswa.2017.09.051.
- Apostol, Tom M. . Springer. 2010: 75–76.
- Rosser, J. Barkley; Schoenfeld, Lowell. . Illinois J. Math. 1962, 6: 64–94.
- ^ Pierre Dusart, "Estimates of some functions over primes without R.H.". arXiv:1002.0442
- ^ Pierre Dusart, "Sharper bounds for ψ, θ, π, pk", Rapport de recherche no. 1998-06, Université de Limoges. An abbreviated version appeared as "The kth prime is greater than k(log k + log log k − 1) for k ≥ 2", Mathematics of Computation, Vol. 68, No. 225 (1999), pp. 411–415.
- ^ Erhard Schmidt, "Über die Anzahl der Primzahlen unter gegebener Grenze", Mathematische Annalen, 57 (1903), pp. 195–204.
- ^ G .H. Hardy and J. E. Littlewood, "Contributions to the Theory of the Riemann Zeta-Function and the Theory of the Distribution of Primes", Acta Mathematica, 41 (1916) pp. 119–196.
- ^ Davenport, Harold (2000). 可見於《Multiplicative Number Theory》一書。 Springer. p. 104. ISBN 0-387-95097-4. Google Book Search.
額外補充
- Apostol, Tom M., , Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, 1976, ISBN 978-0-387-90163-3, MR 0434929, Zbl 0335.10001
外部連結
- 埃里克·韦斯坦因. . MathWorld.
- . PlanetMath.
- . PlanetMath.
- Riemann's Explicit Formula, with images and movies