切比雪夫多项式

第一类切比雪夫多项式由以下递推关系确定

${\displaystyle T_{0}(x)=1\,}$

${\displaystyle T_{1}(x)=x\,}$

${\displaystyle T_{n+1}(x)=2xT_{n}(x)-T_{n-1}(x).\,}$

也可以用母函数表示

${\displaystyle \sum _{n=0}^{\infty }T_{n}(x)t^{n}={\frac {1-tx}{1-2tx+t^{2}}}.}$

第二类切比雪夫多项式由以下递推关系给出

${\displaystyle U_{0}(x)=1\,}$

${\displaystyle U_{1}(x)=2x\,}$

${\displaystyle U_{n+1}(x)=2xU_{n}(x)-U_{n-1}(x).\,}$

此时母函数为

${\displaystyle \sum _{n=0}^{\infty }U_{n}(x)t^{n}={\frac {1}{1-2tx+t^{2}}}.}$

切比雪夫多项式

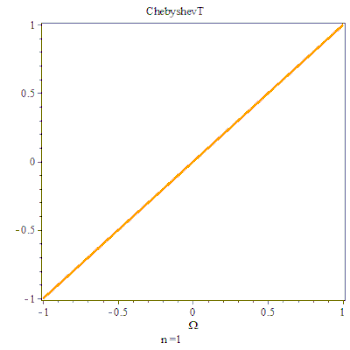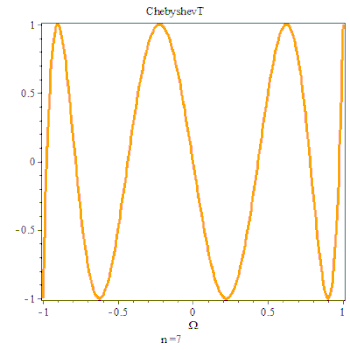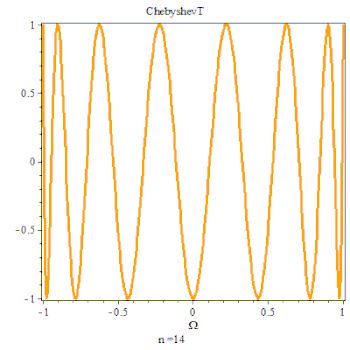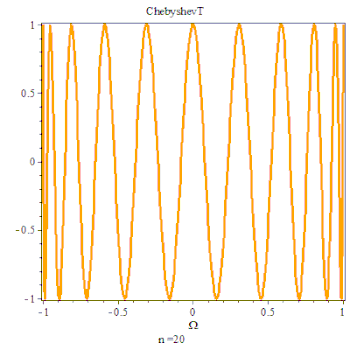
第一类切比雪夫多项式由以下三角恒等式确定

${\displaystyle T_{n}(\cos(\theta ))=\cos(n\theta )\,}$

其中 n = 0, 1, 2, 3, .... . ${\displaystyle \cos n\theta \,}$ 是关于 ${\displaystyle \cos \theta \,}$ 的 n次多项式，这个事实可以这么看： ${\displaystyle \cos n\theta \,}$是:${\displaystyle (\cos \theta +i\sin \theta )^{n}=e^{in\theta }=\cos(n\theta )+i\sin n\theta \,}$的实部（参见棣莫弗公式），而从左边二项展开式可以看出实部中出现含${\displaystyle \sin \theta \,}$的项中，${\displaystyle \sin \theta \,}$都是偶数次的，从而可以表示成 ${\displaystyle 1-\cos ^{2}\theta \,}$的幂 。

用显式来表示

${\displaystyle T_{n}(x)={\begin{cases}\cos(n\arccos(x)),&\ x\in [-1,1]\\\cosh(n\,\mathrm {arccosh} (x)),&\ x\geq 1\\(-1)^{n}\cosh(n\,\mathrm {arccosh} (-x)),&\ x\leq -1\\\end{cases}}}$

尽管能经常碰到上面的表达式，但如果借助于复函数cos(z), cosh(z)以及他们的反函数，则有

${\displaystyle {\begin{matrix}T_{n}(x)&=&\cos(n\arccos(x))\\&=&\mathrm {cosh} (n\,\mathrm {arccosh} (x))\end{matrix}}\ ,\quad \forall x\in \mathbb {R} .}$

类似，第二类切比雪夫多项式满足

${\displaystyle U_{n}(\cos(\theta ))={\frac {\sin((n+1)\theta )}{\sin \theta }}.}$

切比雪夫多项式可被定义为佩尔方程

${\displaystyle T_{i}^{2}-(x^{2}-1)U_{i-1}^{2}=1\,\!}$

在多项式环R[x] 上的解(e.g., 见 Demeyer (2007), p.70). 因此它们的表达式可通过解佩尔方程而得出:

${\displaystyle T_{i}+U_{i-1}{\sqrt {x^{2}-1}}=(x+{\sqrt {x^{2}-1}})^{i}.\,\!}$

两类切比雪夫多项式可由以下双重递归关系式中直接得出:

${\displaystyle T_{0}(x)=1}$

${\displaystyle U_{-1}(x)=1}$

${\displaystyle T_{n+1}(x)=xT_{n}(x)-(1-x^{2})U_{n-1}(x)}$

${\displaystyle U_{n}(x)=xU_{n-1}(x)+T_{n}(x)}$

证明的方式是在下列三角关系式中用${\displaystyle \cos \vartheta }$ 代替${\displaystyle x}$

${\displaystyle T_{n+1}(x)=T_{n+1}(\cos \vartheta )={}}$${\displaystyle \cos((n+1)\vartheta )={}}$${\displaystyle \cos(n\vartheta )\cos \vartheta -\sin(n\vartheta )\sin \vartheta ={}}$${\displaystyle T_{n}(\cos \vartheta )\cos \vartheta -U_{n-1}(\cos \vartheta )\sin ^{2}\vartheta ={}}$${\displaystyle xT_{n}(x)-(1-x^{2})U_{n-1}(x)}$

T_n 和U_n 都是区间[−1,1] 上的正交多项式系.

第一类切比雪夫多项式带权

${\displaystyle {\frac {1}{\sqrt {1-x^{2}}}},}$

即:

${\displaystyle \int _{-1}^{1}T_{n}(x)T_{m}(x)\,{\frac {dx}{\sqrt {1-x^{2}}}}=\left\{{\begin{matrix}0&:n\neq m~~~~~\\\pi &:n=m=0\\\pi /2&:n=m\neq 0\end{matrix}}\right.}$

可先令x= cos(θ) 利用 T_n (cos(θ))=cos(nθ)便可证明.

类似地，第二类切比雪夫多项式带权

${\displaystyle {\sqrt {1-x^{2}}}}$

即:

${\displaystyle \int _{-1}^{1}U_{n}(x)U_{m}(x){\sqrt {1-x^{2}}}\,dx={\begin{cases}0&:n\neq m\\\pi /2&:n=m\end{cases}}}$

其正交化后形成的随机变量是 Wigner 半圆分布).

对每个非负整数${\displaystyle n}$， ${\displaystyle T_{n}(x)}$ 和 ${\displaystyle U_{n}(x)}$ 都为 ${\displaystyle n}$次多项式。 并且当${\displaystyle n}$为偶（奇）数时，它们是关于${\displaystyle x}$ 的偶（奇）函数， 在写成关于${\displaystyle x}$的多项式时只有偶（奇）次项。

${\displaystyle n\geq 1}$时，${\displaystyle T_{n}}$ 的最高次项系数为 ${\displaystyle 2^{n-1}}$ ，${\displaystyle n=0}$时系数为${\displaystyle 1}$ 。

对${\displaystyle n\geq 1}$，在所有最高次项系数为1的${\displaystyle n}$次多项式中 ， ${\displaystyle f(x)={\frac {1}{2^{n-1}}}T_{n}(x)}$ 对零的偏差最小，即它是使得${\displaystyle f(x)}$在${\displaystyle [-1,1]}$ 上绝对值的最大值最小的多项式。 其绝对值的最大值为${\displaystyle {\frac {1}{2^{n-1}}}}$ ， 分别在${\displaystyle -1}$ 、 ${\displaystyle 1}$ 及 ${\displaystyle f}$ 的其他 ${\displaystyle n-1}$ 个极值点上达到 。

两类切比雪夫多项式间还有如下关系：

${\displaystyle {\frac {d}{dx}}\,T_{n}(x)=nU_{n-1}(x){\mbox{ , }}n=1,\ldots }$

${\displaystyle T_{n}(x)={\frac {1}{2}}(U_{n}(x)-\,U_{n-2}(x)).}$

${\displaystyle T_{n+1}(x)=xT_{n}(x)-(1-x^{2})U_{n-1}(x)\,}$

${\displaystyle T_{n}(x)=U_{n}(x)-x\,U_{n-1}(x).}$

切比雪夫多项式是超球多项式或盖根堡多项式的特例, 后者是雅可比多项式的特例.

切比雪夫多项式导数形式的递推关系可以由下面的关系式推出：

${\displaystyle 2T_{n}(x)={\frac {1}{n+1}}\;{\frac {d}{dx}}T_{n+1}(x)-{\frac {1}{n-1}}\;{\frac {d}{dx}}T_{n-1}(x){\mbox{ , }}\quad n=1,2,\ldots }$

前六个第一类切比雪夫多项式的图像，其中-1¼<x<1¼, -1¼<y<1¼; 按颜色依次是T₀, T₁, T₂, T₃, T₄ T₅.

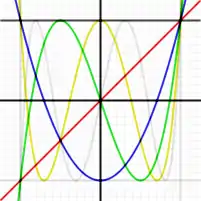
前几个第一类切比雪夫多项式是

${\displaystyle T_{0}(x)=1\,}$

${\displaystyle T_{1}(x)=x\,}$

${\displaystyle T_{2}(x)=2x^{2}-1\,}$

${\displaystyle T_{3}(x)=4x^{3}-3x\,}$

${\displaystyle T_{4}(x)=8x^{4}-8x^{2}+1\,}$

${\displaystyle T_{5}(x)=16x^{5}-20x^{3}+5x\,}$

${\displaystyle T_{6}(x)=32x^{6}-48x^{4}+18x^{2}-1\,}$

${\displaystyle T_{7}(x)=64x^{7}-112x^{5}+56x^{3}-7x\,}$

${\displaystyle T_{8}(x)=128x^{8}-256x^{6}+160x^{4}-32x^{2}+1\,}$

${\displaystyle T_{9}(x)=256x^{9}-576x^{7}+432x^{5}-120x^{3}+9x.\,}$

前六个第二类切比雪夫多项式的图像，其中-1¼<x<1¼, -1¼<y<1¼; 按颜色依次是U₀, U₁, U₂, U₃, U₄ U₅. 虽然图像中无法显示,我们实际有 U_n(1)=n+1 以及 U_n(-1)=(n+1)(-1)ⁿ.

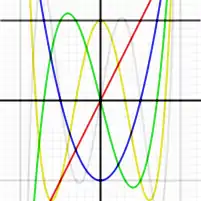
前几个第二类切比雪夫多项式是

${\displaystyle U_{0}(x)=1\,}$

${\displaystyle U_{1}(x)=2x\,}$

${\displaystyle U_{2}(x)=4x^{2}-1\,}$

${\displaystyle U_{3}(x)=8x^{3}-4x\,}$

${\displaystyle U_{4}(x)=16x^{4}-12x^{2}+1\,}$

${\displaystyle U_{5}(x)=32x^{5}-32x^{3}+6x\,}$

${\displaystyle U_{6}(x)=64x^{6}-80x^{4}+24x^{2}-1.\,}$

第一类切比雪夫多项式前几阶导数是

${\displaystyle T_{n}'(1)=n^{2}\,}$

${\displaystyle T_{n}'(-1)=-(-1)^{n}*n^{2}\,}$

${\displaystyle T_{n}''(1)=(n^{4}-n^{2})/3\,}$

${\displaystyle T_{n}''(-1)=(-1)^{n}*(n^{4}-n^{2})/3\,}$

一个N 次多项式按切比雪夫多项式的展开式为如下：

${\displaystyle p(x)=\sum _{n=0}^{N}a_{n}T_{n}(x)}$

多项式按切比雪夫多项式的展开可以用 Clenshaw递推公式计算。

两类的n次切比雪夫多项式在区间[−1,1]上都有n 个不同的根, 称为切比雪夫根, 有时亦称做 切比雪夫节点 ，因为是多项式插值时的 插值点 . 从三角形式中可看出T_n 的n个根分别是：

${\displaystyle x_{i}=\cos \left({\frac {2i-1}{2n}}\pi \right){\mbox{ , }}i=1,\ldots ,n.}$

类似地， U_n 的n个根分别是：

${\displaystyle x_{i}=\cos \left({\frac {i}{n+1}}\pi \right){\mbox{ , }}i=1,\ldots ,n.}$

• 切比雪夫节点
• 切比雪夫滤波器

• M. Abramowitz and I. A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Chapter 22. New York: Dover, 1972.