棣莫弗公式
棣莫弗公式是一個關於複數和三角函數的公式,命名自法國數學家亞伯拉罕·棣美弗(1667年-1754年)。其內容為對任意实数和整數,下列性質成立:
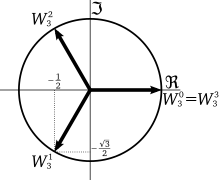
复平面上的立方根等於1.
其中是虛數單位()。值得注意的是,儘管本公式以棣美弗本人命名,他從未直接地將其發表過[1]。為了方便起見,我們常常將合併為另一個三角函數cis(x),也就是說:
在操作上,我們常常限制屬於實數,這樣一來就可藉由比較虛部與實部的方式把和變化為和的形式。另外,儘管棣美弗公式限制須為整數,但倘若適當推廣本公式,便可將拓展到非整數的領域。
證明
(证明的思路是用数学归纳法证明正整数的情形,并推广到负整数。)
令
(1)当时,显然成立。
(2)當时:
左式 右式
因此,成立。
(3)當时:
假設成立,即
當时:
等号1处使用和角公式。
因此,也成立。
综上所述,根據數學歸納法,,成立。
另外,由恒等式:
可知,公式对于负整数情况也成立。
证毕。
用棣莫弗公式求根
此定理可用來求單位複數的 次方根。設 ,表為
若 ,則 也可以表成:
按照棣莫弗公式:
於是得到
- (其中 )
也就是:
當 取 ,我們得到 個不同的根:
參考資料
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.