勒讓德猜想
勒讓德猜想是阿德里安-马里·勒让德提出對整數的猜想,其內容是在平方數和之間,至少有一個質數。此猜想是蘭道問題(1912年)中有關質數的一個問題。截至2023年為止,還沒有人可以證明此猜想成立,也沒有人找到此猜想的反證。
| 未解決的數學問題:在和之間,是否總有質數? |
質數間隙
若勒讓德猜想為真,那在大O符号的意義下,質數p及相鄰質數的最大間隙就會是。[lower-alpha 1]
這猜想是一類與質數間隙相關的猜想和結果的其中一員。其他屬於這一類的猜想和結果包括了已經得證並認為在和必存在一個質數的伯特蘭-切比雪夫定理、尚未得證並認為在、及等之間存在質數的Oppermann猜想、尚未得證並與兩相鄰質數間是否存在質數相關的Andrica猜想和布羅卡猜想,以及尚未得證並認為質數間隙總是遠小於勒讓德猜想且和成比例的克拉梅爾猜想等等。
在克拉梅爾猜想成立的狀況下,勒讓德猜想對任何足夠大的都成立。另外,哈拉爾德·克拉梅爾還證明了一個較弱的結果說,從黎曼猜想可推出最大質數間隙的上界為。[1]
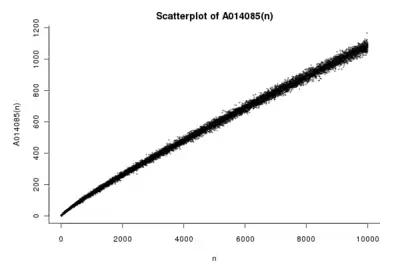
根據質數定理,介於和之間的質數的數量的期望值大約為;此外,已知對幾乎所有的此類區間而言,其實際的質數個數(A014085)與這期望值呈現非病態關係。[2]由於對於較大的而言,這數字也會很大之故,這提供了勒讓德猜想成立的證據。[3]
另外已知質數定理可無條件地[4]或在黎曼猜想成立的狀況下[5],給出對短區間內質數個數的精確估計;然而已證明可行的區間大小大於兩個完全平方數構成的區間,因此就勒讓德猜想而言依舊太大。
部分結果
從英漢對質數間隙的結果可得出,對於足夠大的而言,在完全立方數及之間總有一個質數。[6]
Baker、Harman 和Pintz證明了說對於所有大的而言,這區間內總有一個質數。[7]
利用最大質數間隙表,可確認說勒讓德猜想至少對大到的數都成立,也就是說勒讓得猜想對大到的數都成立。[8]
參考資料
- Stewart, Ian, , Basic Books: 164, 2013, ISBN 9780465022403.
- Bazzanella, Danilo, (PDF), Archiv der Mathematik, 2000, 75 (1): 29–34, MR 1764888, S2CID 16332859, doi:10.1007/s000130050469
- Francis, Richard L., , Missouri Journal of Mathematical Sciences (University of Central Missouri, Department of Mathematics and Computer Science), February 2004, 16 (1): 51–57, doi:10.35834/2004/1601051
 ; see p. 52, "It appears doubtful that this super-abundance of primes can be clustered in
such a way so as to avoid appearing at least once between consecutive squares."
; see p. 52, "It appears doubtful that this super-abundance of primes can be clustered in
such a way so as to avoid appearing at least once between consecutive squares." - Heath-Brown, D. R., (PDF), Journal für die Reine und Angewandte Mathematik, 1988, 1988 (389): 22–63, MR 0953665, S2CID 118979018, doi:10.1515/crll.1988.389.22
- Selberg, Atle, , Archiv for Mathematik og Naturvidenskab, 1943, 47 (6): 87–105, MR 0012624
- A060199
- Baker, R. C.; Harman, G.; Pintz, J., (PDF), Proceedings of the London Mathematical Society, 2001, 83 (3): 532–562, S2CID 8964027, doi:10.1112/plms/83.3.532
- Oliveira e Silva, Tomás; Herzog, Siegfried; Pardi, Silvio, (PDF), Mathematics of Computation, 2014, 83 (288): 2033–2060, MR 3194140, doi:10.1090/S0025-5718-2013-02787-1
 .
.