Firoozbakht猜想
在數論中,Firoozbakht猜想(Firoozbakht's conjecture或Firoozbakht conjecture[1][2])是數學上關於質數分布的一個猜想。這猜想以伊朗數學家Farideh Firoozbakht為名,她在1982年提出此猜想。
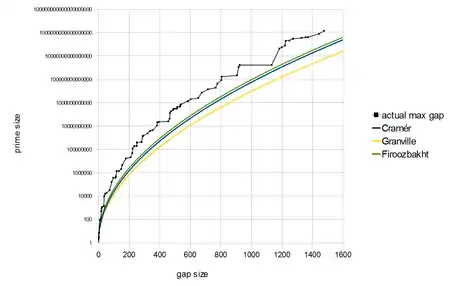
質數間隙函數
這猜想聲稱,是一個嚴格遞減函數(其中是第個質數),也就是說
或等價地
藉由使用最大質數間隙(maximal gap)表,Farideh Firoozbakht確認她的猜想對大到的數都成立。[2]利用廣度更大的最大質數間隙表,目前已知這猜想對任何小於的質數都成立。[3][4]
此外,[6]
對此可見A111943。
這猜想是對質數間隙上界最強的猜想之一,甚至比克拉梅爾猜想和Shanks猜想還強。[4]從這猜想可推出強克拉梅爾猜想,而這與Granville、Pintz[7][8][9]和Maier等人的直觀猜測不一致。[10][11]而這些人的直觀猜測認為,對任意的下式對無限多的數成立:
其中是歐拉-馬斯刻若尼常數。
兩個相關的猜想(可見A182514的討論)如下:
比Firoozbakht猜想來得弱的猜想:
比Firoozbakht猜想來得強的猜想:
註解
- Ribenboim, Paulo.
 . Springer-Verlag. 2004: 185. ISBN 9780387201696.
. Springer-Verlag. 2004: 185. ISBN 9780387201696. - Rivera, Carlos. . [22 August 2012].
- Gaps between consecutive primes
- Kourbatov, Alexei. .
- Sinha, Nilotpal Kanti, , 2010, arXiv:1010.1399
 [math.NT].
[math.NT]. - Kourbatov, Alexei, , Journal of Integer Sequences, 2015, 18 (Article 15.11.2), MR 3436186, Zbl 1390.11105, arXiv:1506.03042
 .
. - Granville, A., (PDF), Scandinavian Actuarial Journal, 1995, 1: 12–28, MR 1349149, Zbl 0833.01018, doi:10.1080/03461238.1995.10413946, (原始内容 (PDF)存档于2016-05-02).
- Granville, Andrew, (PDF), Proceedings of the International Congress of Mathematicians, 1995, 1: 388–399, ISBN 978-3-0348-9897-3, Zbl 0843.11043, doi:10.1007/978-3-0348-9078-6_32.
- Pintz, János, , Funct. Approx. Comment. Math., 2007, 37 (2): 232–471, MR 2363833, S2CID 120236707, Zbl 1226.11096, doi:10.7169/facm/1229619660

- Leonard Adleman and Kevin McCurley, "Open Problems in Number Theoretic Complexity, II" (PS), Algorithmic number theory (Ithaca, NY, 1994), Lecture Notes in Comput. Sci. 877: 291–322, Springer, Berlin, 1994. doi:10.1007/3-540-58691-1_70. ISBN 978-3-540-58691-3.
- Maier, Helmut, , The Michigan Mathematical Journal, 1985, 32 (2): 221–225, ISSN 0026-2285, MR 0783576, Zbl 0569.10023, doi:10.1307/mmj/1029003189

參考資料
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.