升餘弦濾波器

升餘弦濾波器是一種經常用於數位調變的脈衝整形濾波器，它能夠最大限度地減少符碼間干擾（ISI）。之所以會如此命名是因為，該濾波器的最簡形式頻譜（ $\beta =1$ ）的非零部分為餘弦函數，且被「抬升」至水平軸 $f$ 上方。

數學描述

升餘弦濾波器在各種滾降係數下的頻率響應

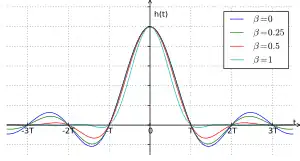
升餘弦濾波器在各種滾降係數下的脈衝響應

升餘弦濾波器是一種低通奈奎斯特濾波器的實作，即具有殘對稱性的濾波器，這表示它的頻譜呈現约 ${\frac {1}{2T}}$ 的奇對稱， $T$ 是通訊系统的符元週期。

其頻域描述為分段定義传递函数，由下式給出：

H(f)={\begin{cases}1,&|f|\leq {\frac {1-\beta }{2T}}\\{\frac {1}{2}}\left[1+\cos \left({\frac {\pi T}{\beta }}\left[|f|-{\frac {1-\beta }{2T}}\right]\right)\right],&{\frac {1-\beta }{2T}}<|f|\leq {\frac {1+\beta }{2T}}\\0,&{\text{otherwise}}\end{cases}}

或以餘的半正矢表示：

H(f)={\begin{cases}1,&|f|\leq {\frac {1-\beta }{2T}}\\\operatorname {hvc} \left({\frac {\pi T}{\beta }}\left[|f|-{\frac {1-\beta }{2T}}\right]\right),&{\frac {1-\beta }{2T}}<|f|\leq {\frac {1+\beta }{2T}}\\0,&{\text{otherwise}}\end{cases}}

0\leq \beta \leq 1

以兩個值為特徵；滾降係數 $\beta$ 和符元率的倒數 $T$ 。

這種濾波器的脈衝響應[1]由下式给出：

h(t)={\begin{cases}{\frac {\pi }{4T}}\operatorname {sinc} \left({\frac {1}{2\beta }}\right),&t=\pm {\frac {T}{2\beta }}\\{\frac {1}{T}}\operatorname {sinc} \left({\frac {t}{T}}\right){\frac {\cos \left({\frac {\pi \beta t}{T}}\right)}{1-\left({\frac {2\beta t}{T}}\right)^{2}}},&{\text{otherwise}}\end{cases}}

以歸一化的sinc函數表示。這裡使用的是通訊領域的定義 $\sin(\pi x)/(\pi x)$ ，而非數學領域所用的定義。

滾降係數

滾降係數 $\beta$ 是對濾波器带宽過量（excess bandwidth）的度量，即所佔带宽超過奈奎斯特頻寬 ${\frac {1}{2T}}$ 的部分，有些作者會使用 $\alpha$ 表示. [2]

若我們將多餘的頻寬表示為 $\Delta f$ ，則：

\beta ={\frac {\Delta f}{\left({\frac {1}{2T}}\right)}}={\frac {\Delta f}{R_{S}/2}}=2T\,\Delta f

$R_{S}={\frac {1}{T}}$ 是符元率。

該圖顯示為 $\beta$ 在0和1之間變化的振幅響應，以及對脈衝響應的相應作用。可以看出，時域的漣波準位會隨著 $\beta$ 減少而增加，這可以減少濾波器的頻寛過量，但只能以伸長脈衝響應為代價。

$\beta =0$

當 $\beta$ 靠近0時，滾降區變得無限窄，因此：

\lim _{\beta \rightarrow 0}H(f)=\operatorname {rect} (fT)

$\operatorname {rect} (\cdot )$ 是矩形函數，所以脈衝響應會趨近 $h(t)={\frac {1}{T}}\operatorname {sinc} \left({\frac {t}{T}}\right)$ .因此，在這種情況下，它會收斂到理想或磚牆濾波器。

$\beta =1$

當 $\beta =1$ ，頻譜的非零部分是純粹的升餘弦，可化簡為：

H(f)|_{\beta =1}=\left\{{\begin{matrix}{\frac {1}{2}}\left[1+\cos \left(\pi fT\right)\right],&|f|\leq {\frac {1}{T}}\\0,&{\text{otherwise}}\end{matrix}}\right.

或

H(f)|_{\beta =1}=\left\{{\begin{matrix}\operatorname {hvc} \left(\pi fT\right),&|f|\leq {\frac {1}{T}}\\0,&{\text{otherwise}}\end{matrix}}\right.

頻寬

升餘弦濾波器的頻寬通常定義為其頻譜的非零正頻率部分的寬度，即：

BW={\frac {R_{S}}{2}}(\beta +1),\quad (0<\beta <1)

自相關函數

升餘弦函數的自相關函數如下：

R\left(\tau \right)=T\left[\operatorname {sinc} \left({\frac {\tau }{T}}\right){\frac {\cos \left(\beta {\frac {\pi \tau }{T}}\right)}{1-\left({\frac {2\beta \tau }{T}}\right)^{2}}}-{\frac {\beta }{4}}\operatorname {sinc} \left(\beta {\frac {\tau }{T}}\right){\frac {\cos \left({\frac {\pi \tau }{T}}\right)}{1-\left({\frac {\beta \tau }{T}}\right)^{2}}}\right]

自相關分析可用於分析各種取樣偏移量結果。

應用

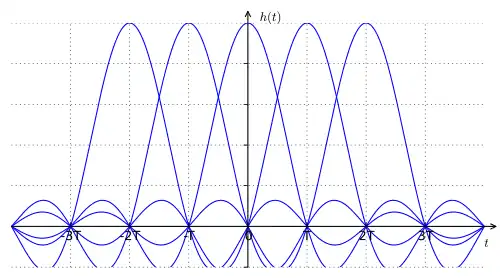
連續升餘弦脈衝，顯示零ISI特性

當用於過濾符元流時，奈奎斯特濾波器具有消除 ISI 的特性，因為除了 $n=0$ 的情形之外，所有 $nT$ （ $n$ 是整數）的脈衝響應都是零。

因此，如果傳輸的波形在接收端被正確採樣，原本的符元值就可以完全恢復。

然而，在許多實際的通訊系統，由於受白雜訊之影響，會在接收器中使用匹配濾波器。對於零 ISI，發射和接收濾波器的淨響應必須等於 $H(f)$ ：

H_{R}(f)\cdot H_{T}(f)=H(f)

因此：

|H_{R}(f)|=|H_{T}(f)|={\sqrt {|H(f)|}}

這些濾波器稱為根升餘弦濾波器。

升餘弦是一種常用於布拉格光纖光柵的變跡濾波器。

參考文獻

(PDF). [2021-08-16]. （原始内容 (PDF)存档于2022-03-28）.
德語： German version of Raised-Cosine-Filter

Glover, I.; Grant, P. (2004). Digital Communications (2nd ed.). Pearson Education Ltd. ISBN 0-13-089399-4.
Proakis, J. (1995). Digital Communications (3rd ed.). McGraw-Hill Inc. ISBN 0-07-113814-5ISBN 0-07-113814-5.
Tavares, L.M.; Tavares G.N. (1998) Comments on "Performance of Asynchronous Band-Limited DS/SSMA Systems" . IEICE Trans. Commun., Vol. E81-B, No. 9

外部連結

Technical article entitled "The care and feeding of digital, pulse-shaping filters" （页面存档备份，存于） originally published in RF Design, written by Ken Gentile.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.