斯涅尔定律
當光波從一種介質傳播到另一種具有不同折射率的介質時,會發生折射現象,其入射角與折射角之間的關係,可以用斯涅尔定律()來描述。斯涅尔定律是因荷兰物理学家威理博·斯涅尔而命名,又稱為「折射定律」。

在光學裏,光線跟蹤科技應用斯涅尔定律來計算入射角與折射角。在實驗光學與寶石學裏,這定律被應用來計算物質的折射率。對於具有負折射率的负折射率超材料(),這定律也成立,允許光波因負折射角而朝後折射。
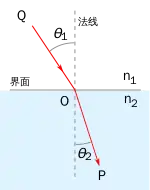
斯涅尔定律表明,當光波從介質1傳播到介质2時,假若兩種介質的折射率不同,則会发生折射現象,其入射光和折射光都處於同一平面,稱為「入射平面」,并且与界面法线的夹角满足如下关系:
- ;
其中,、分别是两種介质的折射率,和分别是入射光、折射光与界面法线的夹角,分别叫做「入射角」、「折射角」。
這公式稱為「斯涅尔公式」。
歷史

最早有系統研究折射問題的學者是住在埃及的希臘人托勒密。西元二世紀,在著作《光學》(Optics)第五卷裏,他提出了他的折射實驗與定律。但是,他從做實驗得到的數據與結論並不準確,沒有給出正弦定律。在那時候,希臘學者不清楚正弦的概念。[1][2]
為巴格達宮廷效勞的伊朗學者伊本·沙爾(Ibn Sahl)在984年的專著《論點火鏡子與透鏡》(On Burning Mirrors and Lenses)裏最先正確地描述折射定律。[3][4]他應用這定律來找出能夠將光聚焦而不會產生幾何像差的透鏡的形狀。這種透鏡稱為曲折透鏡(anaclastic lens)。[5]很可惜的是其它學者並沒有注意到他的研究結果。之後很多年,人們都是從托勒密的錯誤理論開始研究折射。[1]
十一世紀初,阿拉伯學者海什木重做托勒密的實驗。他在著作《光學書》(Kitab al-Manazir, Book of Optics)裏,從做實驗得到的數據,粗略地總結出一些定則。他也沒有得到正弦定律。[6]
1602年,英國天文學者托馬斯·哈里奧特又重新發現了折射定律,可是,他並沒有發表他的結果,雖然他曾經在與约翰内斯·开普勒通信中提到這件事。[7]1621年,斯涅尔推導出一個數學等價形式,但是在他有生之年,學術界並不知道他的成就。勒内·笛卡儿在1637年專著《屈光學》(Dioptrics)裏,獨立地推導出這个定律,並且用他的理論解析了一系列光學問題。在這導引裏,他做了兩個假定,第一個假定是光的傳播速度與介質密度呈正比,第二個假定是光速度沿著界面方向的分量守恆。1662年,皮埃爾·德·費馬發表了另一種導引,從他的版本的最小作用量原理推導出同樣的定律,但是費馬的假定是光的傳播速度與介質密度呈反比。因此,他激烈地反駁笛卡儿的解答,認為笛卡爾的假定有誤。[1]1802年,托馬斯·楊做實驗發現,當光波從較低密度介質傳播到較高密度介质時,光波的波長會變短,他因此推論光波的傳播速度會降低。[8]
根據歷史學者以撒·福雪斯(Issac Vossius)在著作《De natura lucis et proprietate》裏的敘述,笛卡儿先閱讀了斯涅尔的論文,然後調製出自己的導引。有些歷史學者覺得這指控太過誇張,難以置信;但是很多歷史學者都存疑曾經發生了這回事,費馬與惠更斯分別多次重複地譴責笛卡儿的行為缺失。儘管這不名譽事件所造成的風波,在法國,斯涅尔定律被稱為「笛卡儿定律」,或「斯涅尔-笛卡儿定律」
1678年,克里斯蒂安·惠更斯在著作《光論》(Traité de la Lumiere)裏表明,應用惠更斯原理,可以從光的波動性質,解釋或推導出斯涅尔定律。
從费马原理推導

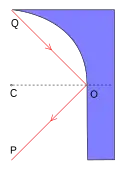
費馬原理又稱為「最短時間原理」:光線傳播的路徑是需時最少的路徑[9]。費馬原理更正確的版本應是「平穩時間原理」。對於某些狀況,光線傳播的路徑所需的時間可能不是最小值,而是最大值,或甚至是拐值。例如,對於平面鏡,任意兩點的反射路徑光程是最小值;對於半橢圓形鏡子,其兩個焦點的光線反射路徑不是唯一的,光程都一樣,是最大值,也是最小值;對於半圓形鏡子,其兩個端點Q、P的反射路徑光程是最大值;又如最右圖所示,對於由四分之一圓形鏡與平面鏡組合而成的鏡子,同樣這兩個點Q、P的反射路徑的光程是拐值。[8]
設定介質1、介質2的折射率分別為、,光線從介質1在點O傳播進入介質2,為入射角,為折射角。

從費馬原理,可以推導出斯涅尔定律。光線在介質1與介質2的速度 和 分別為
- 、
- ;
其中,是真空光速。
由於介質會減緩光線的速度,折射率和都大於。
如右圖所示,從點Q到點P的傳播時間為
- 。
根據費馬原理,光線傳播的路徑是所需時間為極值的路徑,取傳播時間對變數的導數,設定其為零:
- 。
根据正弦函数定义,可以得到傳播速度與折射角的關係式:
- 。
將傳播速度與折射率的關係式代入,就會得到斯涅尔定律:
- 。
從惠更斯原理推導
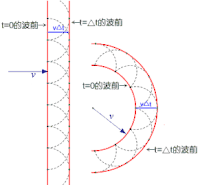
惠更斯原理表明,波前的每一点可以視为产生球面次波的點波源,而以後任何时刻的波前则可看作是正切这些次波的包络。假設傳播速度為的波前,在時間為平面,在這波前的每一點所產生的球面次波,在時間已傳播了距離,由於正切這些球面次波的包络只能為平面,所以波前在時間為平面。波前傳播的方向垂直於這兩個相互平行的平面。

如右圖所示,光波從介質1傳播進入介質2,其入射角、折射角分別為、,傳播速度分別為、,假設。在時間時,光波的波前會包含點和點 的位置,標記這時的波前為。假設時間與之間的間隔為常數,則以下幾個直線段之間的長度相等關係成立:
- 、
- 。
從波前的每一個點波源發射出的球面次波,分別在介質1、介質2的傳播速度為、,必須正切這些球面次波。特別而言,在時間間隔之後,波前在介質1的部分必須平行於相距的波前,而波前在介質2的部分必須正切從點波源發射出的半徑為的球面次波。所以,在通過界面時,會出現彎曲的波前。
由於光波傳播的方向垂直於波前,所以在介質1、介質2裏,波前與界面之間的夾角分別等於入射角、折射角。直線段長度與之間的關係為
- 。
即
- 。
應用折射率的定義式:
- ;
其中,為光速。
總結,斯涅尔定律成立:
- ;
其中,、分別為介質1、介質2的折射率
從平移對稱性推導
假設對某系統整體做一個平移之後,這系統仍舊保持不變,則稱此系統具有平移對稱性。從平移對稱性,可以推導出斯涅尔定律。[10]這是建立於橫向均匀界面不能改變橫向動量的道理。由於波向量與光子的動量成正比,假設介質1、介質2的界面垂直於z-方向,則在介質1、介質2裏的光波橫向傳播方向必須保持不變:
- 、
- 。
因此,
- 。
應用折射率的定義式:
- ;
其中,是光波的角頻率。
總結,斯涅尔定律成立:
- 。
微觀至原子尺寸,雖然沒有任何界面是完全均勻的,假若精細至光波波長尺寸,傳播區域可以估視為均勻,則平移對稱性仍不失為優良近似。
從馬克士威方程組推導
幾何光學的三條基礎定律為
- 第一定律:入射波、反射波、折射波的波向量,與界面的法線共同包含於「入射平面」。
- 第二定律:反射角等於入射角。這定律稱為「反射定律」。
- 第三定律:。這定律稱為「斯涅尔定律」,又稱為「折射定律」。
光波是電磁輻射,必須滿足馬克士威方程組與伴隨的邊界條件,其中一條邊界條件為,在邊界的臨近區域,電場平行於邊界的分量必須具有連續性。假設邊界為xy-平面,則在邊界,
- ;
其中,、、分別為在入射波、反射波、折射波(透射波)的電場平行於邊界的分量。
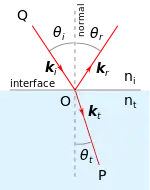
假設入射波是頻率為的單色平面波,則為了在任意時間滿足邊界條件,反射波、折射波的頻率必定為。設定、、的形式為
- 、
- 、
- ;
其中,、、分別是入射波、反射波、折射波的波向量,、、分別是入射波、反射波、折射波的波幅(可能是複值)。
為了在邊界任意位置滿足邊界條件,相位變化必須一樣,必須設定
- 。
因此,
- 、
- 。
不失一般性,假設,則立刻可以推斷第一定律成立,入射波、反射波、折射波的波向量,與界面的法線共同包含於入射平面。
從波向量x-分量的相等式,可以得到
- 。
而在同一介質裏,。所以,第二定律成立,入射角等於反射角。
應用折射率的定義式:
- ,
可以推斷第三定律成立:
- ;
其中,、分別是折射介質的折射率與折射角。
全內反射與臨界角

「光密介質」是折射率比較大的介質;「光疏介质」是折射率比较小的介质。假設光從折射率為的光密介质傳播進入到折射率為的光疏介质(例如,從玻璃傳播進入到空气中),而入射角等於临界角,則折射光线会沿折射界面的切线进行,即折射角。此时会有。因此,可推得
- 。
假若入射角,則無法找到對應的折射角,不存在折射光,而只存在反射光,這現象稱為全内反射。临界角是促使全内反射发生的最小入射角,它的值取决于两种介质的折射率的比值:
- 。
例如,水的折射率为1.33,空气的折射率近似等于1.00,临界角為
- 弧度,即48.8°(角度)。
耗損性、吸收性、導電性介質
在導電性介質裏,電容率與折射率都是複值,連帶的,折射角與波向數都是複值。這意味著,等實相位曲面的法線與界面的法線之間的角度等於折射角,而等波幅曲面是與界面相互平行的平面。由於這兩個曲面通常不會重疊在一起,這種波被稱為「非均勻波」。[12]折射波呈指數衰減,指數與折射率的虚数部分成正比。[8][13]
各向異性物質
對於各向同性或鏡面介質(例如玻璃),通常斯涅尔定律成立。對於各向異性介質,例如,方解石,雙折射會將折射線分為兩束射線,「尋常射線」與「非常射線」。尋常射線照樣遵守斯涅尔定律,而非常射線可能會與入射線不共面。
参阅
- 哈密頓光學(Hamiltonian optics)
- 隱失波(Evanescent wave)
參考文獻
- Grattan-Guinness, Ivor, 1 reprint, illustrated, annotated, JHU Press: pp. 262–264, 2003, ISBN 9780801873966 (英语)
- Ptolemy; Smith, A. Mark, , American Philosophical Society: pp. 42ff, 1996, ISBN 9780871698629 (英语)
- Wolf, K. B. . European Journal of Physics. 1995, 16: 14–20 (英语).
- Rashed, Roshdi. . Isis. 1990, 81 (3): 464–491. doi:10.1086/355456 (英语).
- Sara Cerantola, "La ley física de Ibn Sahl: estudio y traducción parcial de su Kitāb al-ḥarraqāt / The physics law of Ibn Sahl: Study and partial translation of his Kitāb al-ḥarraqāt (页面存档备份,存于)", Anaquel de Estudios Árabes, 15 (2004): 57-95.
- Mihas, Pavlos. (PDF). . University of Leeds, England. July 18, 2005. (原始内容 (PDF)存档于2008年2月29日) (英语).
- Kwan, A., Dudley, J., and Lantz, E. . Physics World. 2002, 15 (4): 64 [2012-06-20]. (原始内容存档于2007-03-03) (英语).
- Hecht, Eugene, 4th, United States of America: Addison Wesley: pp. 106–111, 127–129, 141, 2002, ISBN 0-8053-8566-5 (英语)
- Dugas, R., , New York: Dover Publications, Inc.: pp. 255ff, 274, 345–346, 1988, ISBN 0-486-65632-2 (英语)
- John D Joannopoulos, Johnson SG, Winn JN & Meade RD. 2nd. Princeton NJ: Princeton University Press. 2008: pp. 31 [2012-06-20]. ISBN 978-0-691-12456-8. (原始内容存档于2011-07-22) (英语).
- Griffiths, David J., , Prentice Hall: pp. 386–389, 1998, ISBN 0-13-805326-X (英语)
- Born; Wolf. . (英语).
- Orfanidis, S. J. . (PDF). [2012-06-20]. (原始内容存档 (PDF)于2020-07-30) (英语).