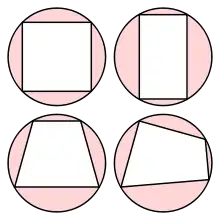
圆内接四边形

在一个圆内接四边形中，相对的两内角是互补的，它们度数之和为180度[1]。与此等价的说法是，圆内接四边形的一个内角等于其相对面的角的外角。一個四邊形為圓內接四邊形的充分必要條件是其相对的两内角互补，即，圆内接四边形相对的两内角互补，且相对的两内角互补的四邊形是圓內接四邊形（四邊形四頂點共圓或說有四邊形有外接圓）。

如图，ABCD为圆内接四边形，托勒密定理指出：${\displaystyle {\begin{matrix}BD\cdot AC\\=AB\cdot CD+BC\cdot DA.\end{matrix}}}$

托勒密定理指出，圆内接四边形的两组对边乘积之和等于两条对角线的乘积（如右图）。对于非退化的四边形，如果两组对边乘积之和等于两条对角线的乘积，那么必定是圆内接四边形[2]。

凸四边形的两条对角线将自身分成四个三角形。如果这个四边形是圆内接四边形，那么相对的两个三角形是相似的。如右图中，${\displaystyle P}$是圆内接四边形${\displaystyle ABCD}$的两对角线交点，则${\displaystyle \bigtriangleup ABP\sim \bigtriangleup DCP}$，${\displaystyle \bigtriangleup BCP\sim \bigtriangleup ADP}$。一个与此等价的说法是所谓的相交弦定理：设凸的圆内接四边形的两条对角线相交于一点(图中的${\displaystyle P}$），那么其中一条对角线被点${\displaystyle P}$所分成的两段的长度之乘积等于另一条对角线被点${\displaystyle P}$所分成的两段的长度之乘积：${\displaystyle AP\times CP=BP\times DP}$。相应的逆命题也成立：如果一个四边形ABCD的两条对角线交于点${\displaystyle P}$，且${\displaystyle \bigtriangleup ABP\sim \bigtriangleup DCP}$（或${\displaystyle \bigtriangleup BCP\sim \bigtriangleup ADP}$，或${\displaystyle AP\times CP=BP\times DP}$），那么四边形${\displaystyle ABCD}$是圆内接四边形。

在四边形中，矩形、正方形都是圆内接四边形；鳶形和梯形可能是圆内接四边形。如果一个四边形既是平行四边形又是圆内接四边形，那么它是一个矩形。如果一个四边形既是梯形又是圆内接四边形，那么它是一个等腰梯形。如果一个鳶形是圆内接四边形，那么它至少有一对对角是直角。

在已知四边的边长时，圆内接四边形的面积可通过婆羅摩笈多公式给出[3]。若圆内接四边形的四边边长分别是${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$, ${\displaystyle d}$，则其面积为：

${\displaystyle {\sqrt {(p-a)(p-b)(p-c)(p-d)}}}$

其中${\displaystyle p}$為半周长：

${\displaystyle p={\frac {a+b+c+d}{2}}.}$

可以证明，在所有周长为定值${\displaystyle 2p}$的圆内接四边形中，面积最大的是正方形。

• 圆内接多边形
• 婆羅摩笈多公式
• 婆羅摩笈多定理：关于对角线相互垂直的圆内接四边形的一个定理。
• 外接圆

1. 欧几里得，《几何原本》第三章，命题22 （页面存档备份，存于）
2. 樂嗣康，托勒密(Ptolemy) 定理與“三弦定理”的關係 （页面存档备份，存于），《數學傳播》26卷1期
3. . [2009-10-19]. （原始内容存档于2008-12-02）.

• （英文）体验圆内接四边形（页面存档备份，存于）
• （英文）关于圆内接四边形的一个定理（页面存档备份，存于）