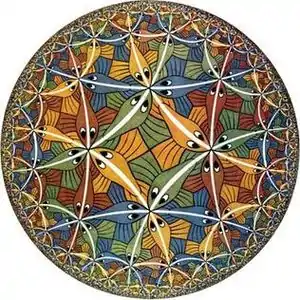
圓極限III

圓極限III（英語：）[1]是M. C. 埃舍爾（M. C. Escher，又譯艾雪）在1959年完成的木刻版畫，該作品被描述為「魚串就像從無限遠射出來的火箭[註 1]」然後「再次降落回他們的出發地[註 2]」[2]。

《圓極限III》, Circle Limit III, 1959

它是一系列埃舍爾所描繪的四個雙曲幾何木刻之一。荷蘭數學物理學家布魯諾·恩斯特稱它是“最好的四個”[3]。

靈感
(6,4,2)三角群雙曲鑲嵌給了艾雪靈感

艾雪在1936年訪問了在西班牙格拉納達與阿罕布拉之後，就對平面鑲嵌有了極大的興趣[4][5]並從他1937年的作品《變形I》開始，人類和動物鑲嵌圖就成為他作品的材料之一[5]。直到1958年艾雪寄了一封信給H. S. M.考克斯特，艾雪寫道他的靈感來自於考克斯特的文章《晶體對稱性及其應用》（Crystal Symmetry and its Generalizations），他開始了一系列圓極限作品的創作[3][4]。考克斯特的圖描繪了由30°-45°-90°直角三角形[註 3]（羅氏三角形）完成的雙曲平面鑲嵌，該鑲嵌可被解釋為描繪鏡射和鏡射準線的基本域[6]。創作了圓極限III的隔年，艾雪又以(6,4,2)三角群的八角化六階正方形鑲嵌再創作了圓極限IV——天堂和地狱，為圓極限系列的最後一件作品。

幾何學
交錯八邊形鑲嵌, 是一種雙曲鑲嵌由正方形與正三角形組成，位於艾雪的圓極限III作品上

艾雪似乎相信他的木刻中的白色曲線，他們平分了每一條在雙曲平面中的雙曲直線的魚，整個雙曲平面被以龐加萊圓盤模型的形式建構在歐幾里得平面上，龐加萊圓盤模型使每條雙曲直線垂直於圓盤的邊界。事實上，艾雪寫道，魚是垂於於邊界移動的[註 4][2]。然而，由於考克斯特證明並沒有面為交替的正方形和正三角形的直線之雙曲結構，如圖所示。相反，白色曲線是滿足角度cos−1((21/4 − 2−1/4)/2)大約80度的邊界圓的超圓形[3]。位於白線中間的紅色三角形和正方形才是真正的雙曲面對稱軸線。木刻的正方形和三角形與雙曲平面鑲嵌的交錯八邊形鑲嵌擁有相同的規律，但他們的幾何形狀是不一樣的：在交錯八邊形鑲嵌中，正方形和三角形的邊是雙曲線段，而在艾雪的版畫，是超圓形的弧線，讓艾雪的平滑曲線只能在交錯八邊形鑲嵌的角落與多邊形鏈對應。正中心正方形中，有四條魚的魚鰭交會在正方形的中心形成了八階三角形鑲嵌的頂點[註 5]，同時有另一個點，由三條魚的魚鰭交會的公共頂點，也是由三條白線的交點，該點構成的它的對偶——正八邊形鑲嵌[3]。類似的由魚構成直線的鑲嵌可以由三角形或正方形以外的多邊形構成的其他雙曲鑲嵌構造，或以三條以上的白色曲線構造於每個交叉處[7]。

包含在木刻的三個最突出的白色曲線之圓形的歐幾里得坐標可以藉由計算2的平方根與3的平方根的有理數逼近來獲得[8]。

對稱性

忽略魚的顏色，這種模式在雙曲平面中，三角形和正方形的中心分別有三倍和四倍的旋轉對稱性，在白色曲線的交點則有三階二面體對稱（正三角形的對稱性）。在約翰·康威的軌形符號這組對稱以433表示。每條魚為這個對稱群提供了基本域。相反的，魚的兩側並不對稱，因為圖形的白色曲線不是反射對稱軸[9][10]。

細節

在圓極限III中，魚被以四種顏色繪製，使每串魚的每一條魚擁有同一種顏色並且讓每個相鄰但不同串的魚擁有不同的顏色。連同用來勾勒出魚的黑色墨水，整體木刻有五種顏色。它是利用5塊木塊製作，每塊提供了四分之一圓盤內的顏色，總計展示了20次，整個作品圓形的直徑是41.5公分[11]。

參見

注釋
  1. strings of fish shoot up like rockets from infinitely far away
  2. fall back again whence they came
  3. 30°-45°-90°直角三角形是一種雙曲幾何圖形，並非平面幾何的圖形，其為一種施瓦茨三角形
  4. the fish move "perpendicularly to the boundary"
  5. 該頂點與八階三角形鑲嵌的頂點的頂點同構，即階為八個不重疊正三角形的公共頂點

參考文獻
  1. 1994 M. C. Escher《Circle Limit III》, 1959, CAordon Art-Baarn-Holland
  2. Escher, as quoted by Coxeter (1979).
  3. Coxeter, H. S. M., , Leonardo, 1979, 12: 19–25, JSTOR 1574078.
  4. Emmer, Michele, , International Journal of Geometric Methods in Modern Physics, 2006, 3 (5-6): 869–879, MR 2264394, doi:10.1142/S0219887806001594.
  5. Schattschneider, Doris, (PDF), Notices of the AMS, 2010, 57 (6): 706–718 [2014-06-17], （原始内容存档 (PDF)于2015-02-23）.
  6. An elementary analysis of Coxeter's figure, as Escher might have understood it, is given by Casselman, Bill, , AMS Feature Column, June 2010 [2014-06-17], （原始内容存档于2014-07-14）. Coxeter expanded on the mathematics of triangle group tessellations, including this one in Coxeter, H. S. M., , Canadian Mathematical Bulletin, 1997, 40 (2): 158–168, MR 1451269, doi:10.4153/CMB-1997-019-0.
  7. Dunham, Douglas, , (PDF), [2014-06-18], （原始内容存档 (PDF)于2014-07-14）.
  8. Coxeter, H. S. M., , , Springer: 297–304, 2003, doi:10.1007/3-540-28849-X_29.
  9. Conway, J. H., , , London Math. Soc. Lecture Note Ser. 165, Cambridge: Cambridge Univ. Press: 438–447, 1992, MR 1200280, doi:10.1017/CBO9780511629259.038. Conway wrote that "The work Circle Limit III is equally intriguing" (in comparison to Circle Limit IV, which has a different symmetry group), and uses is it as an example of this symmetry group.
  10. Herford, Peter, , Zentralblatt fü Didaktik der Mathematik, 1999, 31 (5): 144–148, doi:10.1007/BF02659805. Paper presented to the 8th International Conference on Geometry, Nahsholim (Israel), March 7–14, 1999.
  11. Escher, M. C., , Taschen: 10, 2001 [2014-06-19], （原始内容存档于2014-07-15）.

外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.