直角三角形
有一个角为直角的三角形称为直角三角形(英語:right triangle)。在直角三角形中,直角相邻的两条边称为直角邊。直角所对的边称为斜边。直角三角形直角所对的边也叫作「弦」。若兩條直角邊不一樣長,短的那條邊叫作「勾」,長的那條邊叫作「股」[1]。
| 直角三角形(英語:right triangle) | |
|---|---|
 直角三角形,C為直角,对于角A而言,a為對邊、b為鄰邊、c為斜邊 | |
| 對偶 | 相似的直角三角形 |
| 邊 | 3 |
| 頂點 | 3 |
| 面積 | 兩條直角邊的積除以2 |
| 內角(度) | 90° 、另外兩角和為90° |
直角三角形满足畢氏定理(勾股定理),即两直角边边长的平方和等于斜边长的平方。直角三角形各邊和角之間的關係也是三角學的基礎。
若直角三角形的三邊均為整數,稱為畢氏三角形,其邊長稱為勾股數。
主要性質
面積
和其他三角形相同,直角三角形的面積等於任一邊(底邊)乘以對應高的一半。在直角三角形中.若以一股(直角邊)為底邊,另一股即為對應的高,因此面積為二股直角邊乘積的一半,面積T的公式為
其中a和b是直角三角形的二股。
若內切圓和斜邊AB相切於P點,令半周長為s,則且,面積可表示為
此公式只適用在直角三角形[3]。
高

若在直角三角形有直角的頂點處作往斜邊的高,可以將三角形切割成二個較小的三角形,兩者均和原三角形相似,且二個小三角形彼此相似。因此:
- 高為斜線切割出的二線段的幾何平均數。
- 各股是直角三角形的高和斜線切割出的二線段中相鄰部份的幾何平均數。
若以方程式表示
- (有時稱為直角三角形高定理)
其中, , , , , 均如圖所示[4]:p.156。
三角形的面積等於底邊乘高除二,也等於二股乘積除二,兩者相等,因此
- 。
勾股定理

勾股定理也稱為畢氏定理,內容如下:
在任意直角的三角形中,邊長等於斜邊的正方形,其面積等於邊長等於兩股的二個正方形的和
可以表示為以下的公式表示
其中為斜邊長,而和為剩下二股的長度。
性质
一三角形,其各邊為、半周長、面積、斜邊的高、外接圓半徑、內切圓半徑、旁切圓半徑, , (分別和, , 邊相切)、中線, , ,此三角形為直角三角形若且唯若以下六類的敘述中有任何一個成立。以下的敘述也是直角三角形的性質。
面積
- 其中P為內切圓和最長邊AB相切的點[10]
各邊的比例
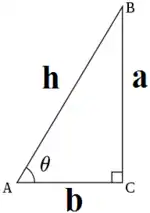
銳角的三角函數可以用直角三角形各邊的比例來定義。針對一特定銳角,可以繪製一直角三角形,各邊分別是此銳角的對邊、鄰邊及斜邊。所有有相同大小銳角的直角三角形都為相似形,因此依照上面的定義,各邊的比例只和此銳角的角度有關。若一角度,其對邊、鄰邊及斜邊分別是, 及,則其三角函數為:
特殊的直角三角形
特定角度的三角函數可以計算其精確值,因此對應直角三角形的各邊比例也可以得知。例如像30°-60°-90°三角形,可以用來計算角度為π/6倍數的三角函數,以及45°-45°-90°三角形,可以用來計算角度為π/4倍數的三角函數,這些都屬於特殊直角三角形。
泰勒斯定理

泰勒斯定理提到若A點是直徑的BC的一圓上的一點,且不和B點及C點共點,ABC為直角三角形,角A為直角。其逆定理為若一三角形內接於一圓,則其斜邊長度即為該圓的直徑。因此可以推論由直角頂邊到斜邊的中線(外接圓半徑)為斜邊的一半。而直角三角形外接圓的半徑為直角頂邊到斜邊的中線長.也是直徑的一半。
其他性質
若長度為及,通過頂點的線段,將斜邊分為三等分,則[14]:pp. 216-217
- 。
除直角三角形以外的三角形都可以找到三個相異的內接正方形,但直角三角形只能找到二個相異的內接正方形[15]。
令和()為一斜邊長為的直角三角形的二個內接正方形邊長,則
直角三角形的周長等於內切圓及三個旁切圓的半徑和。
參看
參考資料
- . 科博館. [2013-08-22]. (原始内容存档于2019-09-15).
- A. Aleksei Petrovich Stakhov. . World Scientific. 2009: p.86. ISBN 9812775838.
- Di Domenico, Angelo S., "A property of triangles involving area", Mathematical Gazette 87, July 2003, pp. 323-324.
- Wentworth, G.A. . Ginn & Co. 1895.
- Voles, Roger, "Integer solutions of ," Mathematical Gazette 83, July 1999, 269–271.
- Richinick, Jennifer, "The upside-down Pythagorean Theorem," Mathematical Gazette 92, July 2008, 313–317.
- . Art of problem solving. 2011-06-11 [2013-08-24]. (原始内容存档于2014-04-28).
- Andreescu, Titu and Andrica, Dorian, "Complex Numbers from A to...Z", Birkhäuser, 2006, pp. 109-110.
- . CTK Wiki Math. 2012-10-17 [2013-08-24]. (原始内容存档于2013-08-05).
- Darvasi, Gyula, , The Mathematical Gazette, March 2005, 89 (514): 72–76.
- Bell, Amy, (PDF), Forum Geometricorum, 2006, 6: 335–342 [2013-08-24], (原始内容存档 (PDF)于2021-08-31).
- Inequalities proposed in “Crux Mathematicorum” (页面存档备份,存于), Problem 954, p. 26, .
- Di Domenico, A., "The golden ratio — the right triangle — and the arithmetic, geometric, and harmonic means," Mathematical Gazette 89, July 2005, 261. Also Mitchell, Douglas W., "Feedback on 89.41", vol 90, March 2006, 153-154.
- Posamentier, Alfred S., and Salkind, Charles T. Challenging Problems in Geometry, Dover, 1996.
- Bailey, Herbert, and DeTemple, Duane, "Squares inscribed in angles and triangles", Mathematics Magazine 71(4), 1998, 278-284.
