垂足三角形
在幾何學上,垂足三角形(英語:)是將一個點投影至三角形的邊上所得到的三角形。

三角形 ABC 為黑色,從 P 延伸出去的三條垂線為藍色,由此得到的垂足三角形 LMN 為紅色
具體地說,考慮一個三角形,選定一個異於頂點的點。通過對三角形的三邊做垂直線,將這些垂直線與的交點分別命名為,則三角形是一個垂足三角形。
相關定理
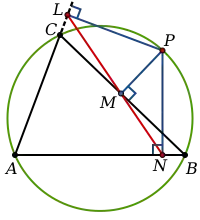
P 在外接圓上的情形,此時垂足三角形退化為一條線(紅色)

卡諾定理:紅色區域與藍色區域的面積相等
西姆松定理
若點位於的外接圓上,則共線,反之亦然。這條線被稱為垂足線(英語:),又稱為西姆松線(英語:)。
反垂足三角形

三角形 ABC 為紅色,從 P 延伸至頂點的三條線為藍色,由此得到的反垂足三角形 LMN 為黑色
過作一條垂直於的直線,過作一條垂直於的直線,過作一條垂直於的直線,則這三條直線構成的三角形稱為反垂足三角形(英語:)。在這個反垂足三角形中,設與相對的頂點為,與相對的頂點為,與相對的頂點為。
是在點上的垂足三角形,這也是其名稱的由來。
若點以三角形為基準的三線坐標是,則反垂足三角形的頂點坐標為:[3]
參考資料
- . en.wikibooks.org. [2020-10-31]. (原始内容存档于2021-08-22).
- Alfred S. Posamentier; Charles T. Salkind. . New York: Dover. 1996: 85-86. ISBN 9780486134864. OCLC 829151719.
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2021-08-22]. (原始内容存档于2021-08-22) (英语).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.