奇函數與偶函數

在數學裡，偶函數（英語：）和奇函數（英語：）是滿足著相對於加法逆元之特定對稱關係的函數。這在數學分析的許多領域中都很重要，特別是在冪級數和傅立葉級數的理論裡。其命名是因為冪函數的冪的奇偶性滿足下列條件：若n為一偶數，則函數 $x^{n}$ 是偶函數，若 $n$ 為一奇數，則為奇函數。

偶函數

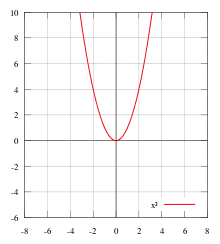
f(x) = x²，偶函數的一個例子

設f(x)為一實變數實值函數，則 $f$ 為偶函數若下列的方程對所有在 $f$ 的定義域內的 $x$ 都成立：[1]

f(x)=f(-x)

幾何上，一個偶函數會关于y軸對稱，亦即其圖像在對y軸為轴对称後不會改變。

偶函數的例子有|x|、x²、x⁴、cos(x)和cosh(x)。

偶函數不可能是個雙射映射。

奇函數

f(x) = x，奇函數的一個例子

再次地，設 $f(x)$ 為一個實變數實值函數，則 $f$ 為奇函數若下列的方程對所有在f的定義域內的 $x$ 都成立：[2]

f(x)=-f(-x)

或

f(-x)=-f(x)

幾何上，一個奇函數关于原點對稱，亦即其圖像在繞原點做180度旋轉後不會改變。

奇函數的例子有 $x$ 、sin(x)、sinh(x)和erf(x)。

基本特性

注意：一個函數為奇函數或偶函數不表示其為可微的，或即使為連續的。其包含在傅立葉級數、泰勒級數、導數等之性質都只在假設其存在時才被使用。

唯一一個同時為奇函數及偶函數的函數為其值為0的常數函數(即對所有 $x$ ， $f(x)=0$ )。
通常，一個偶函數和一個奇函數的相加不會是奇函數也不會是偶函數；如 $x+x^{2}$ 。
兩個偶函數的相加為偶函數，且一個偶函數的任意常數倍亦為偶函數。（偶+偶=偶 n×偶=偶）
兩個奇函數的相加為奇函數，且一個奇函數的任意常數倍亦為奇函數。（奇+奇=奇 n×奇=奇）
兩個偶函數的乘積為一個偶函數。（偶×偶=偶）
兩個奇函數的乘積為一個偶函數。（奇×奇=偶）
一個偶函數和一個奇函數的乘積為一個奇函數。（偶×奇=奇）
兩個偶函數的商（除數不得為0）為一個偶函數。（偶÷偶=偶）
兩個奇函數的商（除數不得為0）為一個偶函數。(奇÷奇=偶)
一個偶函數和一個奇函數的商（除數不得為0）為一個奇函數。（偶÷奇=奇奇÷偶=奇）
一個偶函數的導數為一個奇函數。（偶'=奇）
一個奇函數的導數為一個偶函數。（奇'=偶）
兩個奇函數的複合為一個奇函數，而兩個偶函數的複合為一個偶函數。[奇(奇)=奇偶(偶)=偶]
一個偶函數和一個奇函數的複合為一個偶函數。[偶(奇)=偶奇(偶)=偶]

級數

一個偶函數的麥克勞倫級數只包括偶數冪。
一個奇函數的麥克勞倫級數只包括奇數冪。
一個週期偶函數的傅立葉級數只包括cos項。
一個週期奇函數的傅立葉級數只包括sin項。

代數結構

偶函數的任何線性組合皆為偶函數，且偶函數會形成一個實數上的向量空間。相似地，奇函數的任何線性組合皆為奇函數，且奇函數亦會形成一個實數上的向量空間。實際上，「所有」實值函數之向量空間為偶函數和奇函數之子空間的直和。換句話說，每個定义域关于原点对称的函數都可以被唯一地寫成一個偶函數和一個奇函數的相加： $f(x)=f_{\mathrm {even} }(x)+f_{\mathrm {odd} }(x)={\frac {f(x)+f(-x)}{2}}\,+\,{\frac {f(x)-f(-x)}{2}}$

偶函數會形成一個實數上的可交換代數，但奇函數則不會形成任何一個在實數上的代數。

諧波

在信號處理裡，諧波失真會產生於當一個正弦波信號被一非線性傳遞函數放大的時候。其諧波的類型會因傳遞函數的不同而不同：[3][4]

當傳遞函數為偶函數，其輸出信號會只包括輸入正弦波的偶諧波； $2f,4f,6f,\dots$ $2f,4f,6f,\dots$
- 其基頻亦為一個奇諧波，故將不會出現在輸出信號裡。
- 一個簡單的例子為全波整流器。
當傳遞函數為奇函數時，其輸出信號會只包括輸入正弦波的奇諧波； $1f,3f,5f,\dots$ $1f,3f,5f,\dots$
- 其輸出信號將會有半波對稱。
- 一個簡單的例子為在一個對稱推挽式放大器內的截波。
當傳遞函數為不對稱時，其輸出信號會包括偶諧波或奇諧波； $1f,2f,3f,\dots$ $1f,2f,3f,\dots$
- 一個簡單的例子為在一個不對稱A類放大器內的截波。

参考文献

引用

Gelfand 2002, p. 11
Gelfand 2002, p. 72
. [2006-12-25]. （原始内容存档于2018-01-01）.
Berners, Dave. . UA WebZine. Universal Audio. October 2005 [2016-09-22]. （原始内容存档于2018-01-01）. To summarize, if the function f(x) is odd, a cosine input will produce no even harmonics. If the function f(x) is even, a cosine input will produce no odd harmonics (but may contain a DC component). If the function is neither odd nor even, all harmonics may be present in the output.

来源

书籍

Gelfand, I. M.; Glagoleva, E. G.; Shnol, E. E. . Mineola, NY: Dover Publications. 2002 [1969]. （原始内容存档于2016-09-21）.

参见

埃爾米特函數：在複數上的推广
泰勒級數
傅里葉級數

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Gelfand 2002, p. 11

[2] Gelfand 2002, p. 72

[3] . [2006-12-25]. （原始内容存档于2018-01-01）.

[4] Berners, Dave. . UA WebZine. Universal Audio. October 2005 [2016-09-22]. （原始内容存档于2018-01-01）. To summarize, if the function f(x) is odd, a cosine input will produce no even harmonics. If the function f(x) is even, a cosine input will produce no odd harmonics (but may contain a DC component). If the function is neither odd nor even, all harmonics may be present in the output.