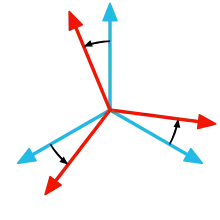
旋转
旋转在几何和线性代数中是描述刚体围绕一个固定点的运动的在平面或空间中的变换。旋转不同于没有固定点的平移,和翻转变换的形体的反射。旋转和上面提及的变换是等距的,它们保留在任何两点之间的距离在变换之后不变。
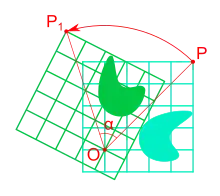
绕点的二维旋转。
二维空间

在绕一个点旋转之后绕另一个不同的点的平面旋转导致要么是旋转(如本图)要么是平移的一个总和运动。
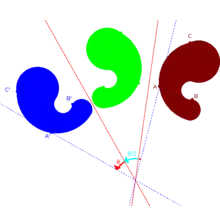
在针对一个轴的反射之后的针对不平行于前一个轴的反射导致是绕两个轴的交点的旋转的一个总和运动。
在讨论旋转的时候理解参照系是重要的。一种观点来看,你可以保持坐标轴固定旋转向量。而从另一观点出发,你可以保持向量固定旋转坐标系。
在第一种观点看来,坐标或向量关于原点的逆时针旋转;或者从第二种观点看来,平面或轴关于原点的顺时针旋转。这里的被旋转了并希望知道旋转后的坐标:
或
平面或轴关于原点的逆时针旋转,在新平面中的坐标将顺时针旋转到旧坐标。在这种情况下,如果在旧平面中的坐标是,同一个向量在新平面中的坐标是,则:
或
向量的大小同于向量 的大小(正交变换是保距映射)。
一个是点的旋转,坐标系没动,得到的是:动的点在原来坐标系下的表示。
另一个是坐标系的旋转,点是不动的,得到的是:不动的点在动了的坐标系下的表示。
坐标或向量关于原点的逆时针旋转平面或轴关于原点的顺时针旋转。
坐标或向量关于原点的顺时针旋转平面或轴关于原点的逆时针旋转。
顺时针(逆时针)旋转可以理解为逆时针(顺时针)旋转一个负角度,根据 , 的奇偶性,即 , 可在逆时针旋转和顺时针旋转的变换公式之间相互转换。
一般化
正交矩阵
描述旋转的所有矩阵的集合M(v,θ)加上矩阵乘法运算叫做旋转群:SO(3)。
注解
- Lounesto 2001, p.30.
引用
- Hestenes, David. . Dordrecht: Kluwer Academic Publishers. 1999. ISBN 0-7923-5514-8.
- Lounesto, Pertti. . Cambridge: Cambridge University Press. 2001. ISBN 978-0-521-00551-7.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.