小角度近似

圖1和圖2可以看出此近似的精度。在角度趨近零時，原始函數和近似函數的差也趨近零。

• 
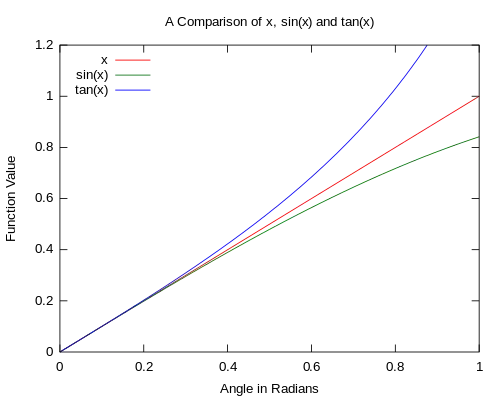  圖1：基本的奇三角函數的比較，當角度θ趨近0時，近似函數很接近原函數。
• 
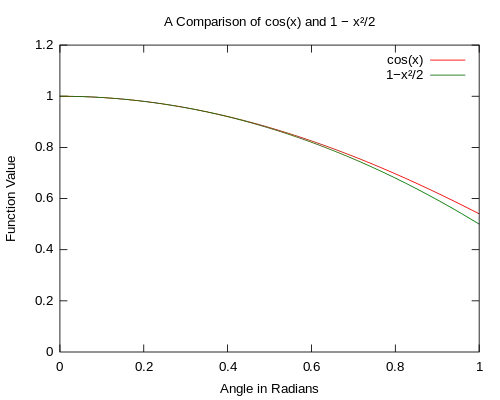  圖2：cos θ和1 − θ²/2的比較。當角度θ趨近0時，兩函數相當接近。

右圖中紅色部份d，是斜邊長度H和鄰邊長度A的差。如圖所示，H和A幾乎一樣長，意思是cos θ接近1，利用θ²/2可以減去紅色的部份

${\displaystyle \cos {\theta }\approx 1-{\frac {\theta ^{2}}{2}}}$。

其對邊O長度近似於藍色圓弧的長度s。根據幾何學，s = Aθ，根據三角函數，sin θ = O/H和tan θ = O/A，根據圖上O ≈ s且H ≈ A可得：

${\displaystyle \sin \theta ={\frac {O}{H}}\approx {\frac {O}{A}}=\tan \theta ={\frac {O}{A}}\approx {\frac {s}{A}}={\frac {A\theta }{A}}=\theta .}$

簡化後可得

${\displaystyle \sin \theta \approx \tan \theta \approx \theta .}$

利用夾擠定理[4]，可以證明 ${\textstyle \lim _{\theta \to 0}{\frac {\sin(\theta )}{\theta }}=1,}$這是在小角度θ時，${\displaystyle \sin(\theta )\approx \theta }$近似式的正式敘述。

比較小心的應用夾擠定理可得 ${\textstyle \lim _{\theta \to 0}{\frac {\tan(\theta )}{\theta }}=1,}$，因此可以得到在小角度θ時，${\displaystyle \tan(\theta )\approx \theta }$。

最後，利用洛必达法则可得${\textstyle \lim _{\theta \to 0}{\frac {\cos(\theta )-1}{\theta ^{2}}}=\lim _{\theta \to 0}{\frac {-\sin(\theta )}{2\theta }}=-{\frac {1}{2}},}$可以整理為${\textstyle \cos(\theta )\approx 1-{\frac {\theta ^{2}}{2}}}$，在小角度θ時成立。也可以用倍角公式${\displaystyle \cos 2A\equiv 1-2\sin ^{2}A}$。令${\displaystyle \theta =2A}$，可得${\textstyle \cos \theta =1-2\sin ^{2}{\frac {\theta }{2}}\approx 1-{\frac {\theta ^{2}}{2}}}$。

正弦函數的小角度近似

將正弦函數進行馬克勞林展開（在零附近的泰勒展開）可得[5]

${\displaystyle {\begin{aligned}\sin \theta &=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}\theta ^{2n+1}\\&=\theta -{\frac {\theta ^{3}}{3!}}+{\frac {\theta ^{5}}{5!}}-{\frac {\theta ^{7}}{7!}}+\cdots \end{aligned}}}$

其中θ是以弧度表示的角度，上式也可以改寫如下：

${\displaystyle \sin \theta =\theta -{\frac {\theta ^{3}}{6}}+{\frac {\theta ^{5}}{120}}-{\frac {\theta ^{7}}{5040}}+\cdots }$

可以看出在θ很小時，第二項（三次方項）會非常小。用θ為0.01為例，第二項的數量級為第一項的 6994100000000000000♠0.000001或1/7004100000000000000♠10000。因此可以單純的近似為：

${\displaystyle \sin \theta \approx \theta }$

另外，因為小角度的餘弦函數接近1，因此正切函數（正弦函數除以餘弦函數）可以表示如下

${\displaystyle \tan \theta \approx \sin \theta \approx \theta }$,

在天文學上，天體的角直徑多半只有幾個角秒，其角度很小，因此可以用小角度近似[6]。線性大小（D）和角直徑（X）以及與觀察者距離（d）之間有以下的公式：

${\displaystyle D=X{\frac {d}{206\,265}}}$

其中X是用角秒表示。

數字7005206265000000000♠206265是圓用角秒表示的值（7006129600000000000♠1296000），除以2π。

精確的公式是

${\displaystyle D=d\tan \left(X{\frac {2\pi }{1\,296\,000}}\right)}$

若tan X改為X，上式也適用。

在計算擺的势能时，二次餘弦近似非常的好用，可以應用在拉格朗日力学上，找到運動的間接方程（能量方程）。

在計算擺的頻率時，可以用正弦函數的小角度近近，將擺的微分方程轉換為簡諧運動的微分方程。

在光學上，小角度近似是近軸近似的基礎。

正弦和正切的小角度近似可以用在雙縫實驗或衍射光栅中，以簡化計算[7]。

小角度近似常用在結構力學上，特別是和穩定性和分岔分析上（主要是軸向受壓力的柱，是否會產生挫曲的分析）。這部份簡化的程度很大。不過不過用在精確的分析上。

空中導航中的1 in 60 rule就是以小角度近似為基礎，加上一個弧度近似於60度的事實。

小角度的和角和差角公式可以在三角函數表的插值：

例如：sin(0.755)

sin(0.755)	= sin(0.75 + 0.005)
	≈ sin(0.75) + (0.005) cos(0.75)
	≈ (0.6816) + (0.005)(0.7317)	[sin(0.75)和cos(0.75)的值是由三角函數表求得]
	≈ 0.6853.