平行軸定理
平行軸定理(英語:parallel axis theorem)能夠很簡易地,從剛體對於一支通過質心的直軸(質心軸)的轉動慣量,計算出剛體對平行於質心軸的另外一支直軸的轉動慣量。
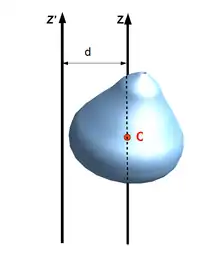
讓 代表剛體對於質心軸的轉動慣量、 代表剛體的質量、 代表另外一支直軸 z'-軸與質心軸的垂直距離。那麼,對於 z'-軸的轉動慣量是
- 。
平行軸定理、垂直軸定理、伸展定則,這些工具都可以用來求得許多不同形狀的物體的轉動慣量。
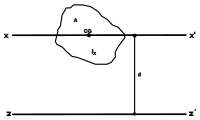
平行軸定理也可以應用於截面二次軸矩(面積慣性矩):
- ;
這裏, 是對於 z-軸的面積慣性矩、 是對於平面質心軸的面積慣性矩、 是面積、 是 z-軸與質心軸的垂直距離。
因雅各·史丹納 () 而命名,史丹納定理所指的幾個理論,其中一個理論就是平行軸定理。
進階理論
平行軸定理能夠很簡易的,從對於一個以質心為原點的座標系統的慣性張量,轉換至另外一個平行的座標系統。
對於三維空間中任意一参考點 Q 與以此参考點為原點的直角座標系 Qxyz ,一個剛體的慣性張量 是
- 。
這裏,對角元素 、 、 分別為對於 x-軸、y-軸、z-軸的慣性矩。設定 為微小質量 對於點 Q 的相對位置。則這些慣性矩,可以精簡地用方程式定義為
- ,
- ,
- 。
而非對角元素,稱為慣性積, 可以定義為
- ,
- ,
- 。
假若已知剛體對於質心 G 的慣性張量 ,質心 G 的位置是 ,則剛體對於原點 O 的慣性張量 ,依照平行軸定理,可以表述為
- ,
- ,
- ,
- ,
- ,
- 。
證明:
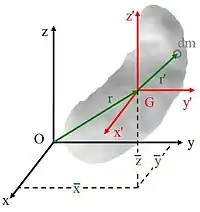
a) 參考右圖 ,讓 、 分別為微小質量 對質心 G 與原點 O 的相對位置:
- , 。
依照慣性張量的慣性矩定義方程式,
- ,
- 。
所以,
相似地,可以求得 、 的方程式。
b) 依照慣性張量的慣性積定義方程式 ,
- ,
- 。
因為 , ,所以
相似地,可以求得對於點 O 的其他慣性積方程式。
實例
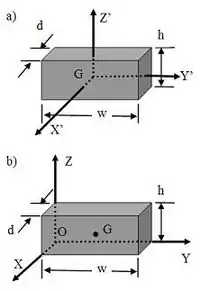
思考一個實心長方體對於質心 G 的慣性張量,
如圖右,質心 G 的位置是 。依照平行軸定理,實心長方體對於點 O 的慣性矩與慣性積分別為
- 、
- 、
- 、
- 、
- 、
- 。
因此,實心長方體對於點 O 的慣性張量是
參閱
- 轉動慣量列表
- 垂直轴定理
參考文獻
- Beer, Ferdinand; E. Russell Johnston, Jr., William E. Clausen (2004). Vector Mechanics for Engineers. 7th edition. USA: McGraw-Hill, ISBN 0-07-230492-8