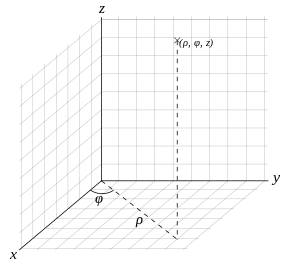
坐標系

數線是最簡單的坐標系，用一個實數標示一個點在線上的位置。數線中會有一個原點O，以及單位長度及其方向。點P的坐標為從O到P的有號距離，坐標是正值或負值則依P點在原點的哪一側來決定。數線上每一個點都有唯一的坐標，每一個實數也都可以在數線上找到唯一的對應點[9]。

The number line

平面的笛卡兒坐標系

笛卡兒坐標系也稱為直角坐標系，是最常用到的一種坐標系。是法國數學家勒內·笛卡尔在1637年發表的《方法論》附錄中提到的[10]。 在平面上，選定二條互相垂直的線為坐標軸，任一點距坐標軸的有號距離為另一軸的坐標，這就是二維的笛卡兒坐標系，一般會選一條指向右方水平線稱為x軸，再選一條指向上方的垂直線稱為y軸，此兩坐標軸設定方式稱為「右手坐標系」。

三維的笛卡兒坐標系

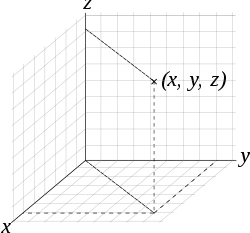
若在三維系統中，選定三條互相垂直的平面，任一點距平面的有號距離為坐標，二平面的交線為坐標軸，即可產生三維的笛卡兒坐標系。一般會選擇x軸及y軸是水平的，z軸垂直往上，且三軸維持右手定則，若先將右手的手掌與手指伸直。然後，將中指指向往手掌的掌面 半空間，與食指呈直角關係。再將大拇指往上指去，與中指，食指都呈直角關係。則大拇指，食指，與中指分別表示了右手坐標系的 x-軸，y-軸，與 z-軸。此概念可以延伸，在n維的欧几里得空间中建立n維的笛卡兒坐標系。

以笛卡兒平面坐標系為基準，右上為第一象限，左上為第二，左下為第三，右下就是第四象限，第一象限的x坐標和y坐標均為正值，第二象限的x坐標為負值，y坐標為正值，第三象限的x坐標和y坐標均為負值，第四象限的x坐標為正值，y坐標為負值[11]，而平面坐標分六大部分，除了四個象限，還有x軸與y軸。在笛卡兒空間坐標系中也可以依xy平面，xz平面及yz平面將不含上述平面空間分為八份，稱為卦限，但一般只定義坐標均大於零的為第一卦限。坐標中的各軸線不屬於象限或卦限。

平面上的極坐標系

極坐標系也是一種常用的平面坐標系統。格雷瓜·德·聖-萬桑特（）在1625年和博納文圖拉·卡瓦列里在1635年，独立地各自引入了极坐标系这一概念。極坐標中會定一點為極點，再將一條通過極點的射線定為極軸。若給定一角度${\displaystyle \theta }$，則可繪出通過極點，和極軸夾角為${\displaystyle \theta }$的唯一射線（角度是以從極軸，依逆時針方向旋轉到射線），若再給定一實數${\displaystyle r}$，可找出上述射線上，距極點距離為有號整數${\displaystyle r}$的一點[12]。

在極坐標系中，一坐標${\displaystyle (r,\theta )}$只會其對應唯一的一點，但每一點均可對應許多個坐標。例如坐標${\displaystyle (r,\theta )}$、${\displaystyle (r,\theta +2\pi )}$及${\displaystyle (-r,\theta +\pi )}$都是對應同一點的不同坐標。而極點的坐標為${\displaystyle (0,\theta )}$，${\displaystyle \theta }$可為任意值。

极坐标${\displaystyle r\,}$和${\displaystyle \theta \,}$可以用下式變換為直角坐标：

${\displaystyle r={\sqrt {y^{2}+x^{2}}}\quad }$（參閱畢氏定理）

${\displaystyle \theta =\operatorname {atan2} (y,x)\quad }$（atan2是已將象限納入考量的反正切函數）

从直角坐标${\displaystyle x\,}$和${\displaystyle y\,}$也可以變換為极坐标：

${\displaystyle x=r\cos \theta \,}$

${\displaystyle y=r\sin \theta \,}$

若將平面上的极坐标系擴展到立體的空間，可擴展為圓柱坐標系及球坐標系。

用圓柱坐標 ${\displaystyle (\rho ,\ \phi ,\ z)}$ 來表示一個點的位置

圓柱坐標系是將极坐标系的 ${\displaystyle (r,\ \theta )}$坐標變成 ${\displaystyle (\rho ,\ \phi )}$ ，再增加一個笛卡爾坐標系的z坐標。如點P的圓柱坐標是${\displaystyle (\rho ,\ \phi ,\ z)}$。

• ${\displaystyle \rho }$是原點至P點在xy-面上投影點之間的距離，也是點P與正z-軸的垂直距離。
• ${\displaystyle \phi }$是線OP在xy-面的投影線與正x-軸之間的方位角。
• ${\displaystyle z}$是點P至點P在xy-面上投影點之間的距離。

直角坐標系和圓柱坐標系的轉換關係如下[13]：

${\displaystyle {x}=\rho \,\cos \phi }$

${\displaystyle {y}=\rho \,\sin \phi }$

${\displaystyle {z}={z}\,}$

用球坐標 ${\displaystyle (r,\ \theta ,\ \phi )}$ 來表示一個點的位置

而球坐標系則是用一個角度 ${\displaystyle \phi }$表示原點到坐標點的連線與正z-軸之間的相對關係。如點P的球坐標為${\displaystyle (r,\ \theta ,\ \phi )}$。

• ${\displaystyle r}$是原點至點P的連線的距離。
• ${\displaystyle \theta }$為原點到點P的連線與正z-軸之間的傾斜角。
• ${\displaystyle \phi }$是線OP在xy-面的投影線與正x-軸之間的方位角。

直角坐標和球坐標系的轉換關係如下[13]：

${\displaystyle x={r}\,\sin \theta \,\cos \phi }$

${\displaystyle y={r}\,\sin \theta \,\sin \phi }$

${\displaystyle z={r}\,\cos \theta }$

在齊次坐標表示時，會增加一個額外的坐標，例如平面上的一點可以表示為${\displaystyle (x,y,z)}$，其中x/z及y/z為其原來在平面上的笛卡爾坐標。其優點是可以在不使用無限大的情形下表示射影平面上的任意點。一般齊次坐標會用在坐標之間的比例比實際的數值來的重要的情形下。

椭圆坐标系，由同焦点的椭圆和双曲线构成的正交坐标系。

以下是其他一些常用的坐標系：

• 曲線坐標系是一種廣義的坐標系，此坐標系是以相交的曲線為基礎。
  • 其中坐标曲面之間的夾角為直角的坐标系称为正交坐标系。
  • 其中坐标曲面之間的夾角不為直角的坐标系称为斜交坐标系。
• 廣義坐標是在處理拉格朗日力學時使用。
• 正則坐標是在處理哈密頓力學時使用。
• 普吕克坐标可以將三維空間中的直線描述為6個齊次坐標。
• 重心坐标一般用在三角图中。
• 平面上的對數-極坐標系是以用一點相對原點的角度及其距離的對數來表示。
• 平行坐標將n-維空間中的一點表示為和n條垂直線有交點的折線。

可有一些描述曲線的方式和坐標系無關，這類的方式會使用本徵方程，其中有用到像是曲率及弧長等不隨坐標系而改變的不變量。這類的本徵方程包括：

• 惠威尔方程和弧長和有關。
• 切薩羅方程和弧長及曲率有關。