康托尔-伯恩斯坦-施罗德定理
施罗德-伯恩斯坦定理(英語:),又称康托尔-伯恩斯坦-施罗德定理()是集合论中的一个基本定理,得名于康托尔、伯恩斯坦和施罗德。该定理陈述说:如果在集合 A 和 B 之间存在单射 f : A → B 和 g : B → A,则存在一个双射 h : A → B。從势的角度來看, 这意味着如果 |A| ≤ |B| 并且 |B| ≤ |A|,则 |A| = |B|,即A与B等势。显然,这是在基数排序中非常有用的特征。
证明
下面是证明:
证明: 令
并令
对任意的 a∈A 定义映射
如果a不在集合C中,那么a不在集合C0中。因此由C0的定义可知a ∈ g[B]。由于g是单射,其逆映射g –1(a)存在。
接下来验证 h : A → B 就是想要的双射。
- 满射:对任何 b ∈ B,如果 b ∈ f[C],那么存在 a ∈ C 使得 b = f(a)。因此由h的定义可知 b = h(a)。如果 b ∉ f[C],定义 a = g(b)。由 C0 的定义知,a 不属于 C0。由于 f[Cn] 是 f[C]的一个子集,因而 b 不属于任何一个 f[Cn]所以由集合Cn的递归定义以及g为单射(不存在b以外的)的事实知,a = g(b) 不属于 Cn+1= g[f[Cn]] (若屬於,則b和f[Cn]可互換)。因此,a 不属于 C(C0和Cn)那么根据h的定义 b = g–1(a) = h(a)。
- 单射:若h(a)=h(b),则有a∈C∧b∈C, a∉C∧b∉C, a∈C∧b∉C, a∉C∧b∈C四种情况。对于前两种情况,由f与g–1是单射得a=b。对于第三种情况,有f(a)=g–1(b)⇒g(f(a))=g(g–1(b))⇒g°f(a)=b,又由前提a∈C,而C在g°f下封闭,于是b∈C,但是由前提得b∉C,矛盾了,因此第三种情况不可能出现。同理,不失一般性,第四种情况也不可能出现,这说明ran(f|C) ∩ ran(g–1|A\C) = ∅。综上若h(a)=h(b),一定有a=b。
注意这个 h 的定义是非构造性的,在這個意義下:不存在一般性方法在有限步骤内判定,对于任何给定集合 A 和 B 与单射 f 和 g,是否 A 的一个元素 x 不位于 C 中。对于特殊集合和映射这当然是可能的。
可视化
h 的定义可透過以下示意图展示。
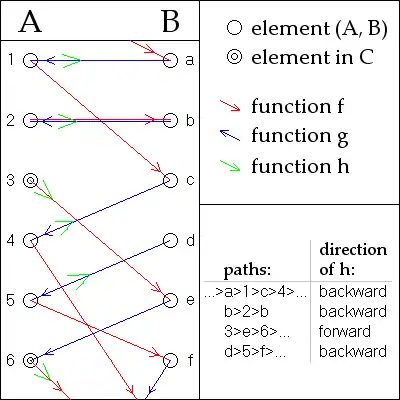
显示的是部分的(不相交)集合 A 和 B ,以及映射 f 和 g的一部分。如果集合 A ∪ B,与两个映射一起,被詮释为一个有向图,则这个双向图有多个连接起来的构件(component)。
这些可以分成四个类型:无限扩展到两个方向的路径,偶数长度的有限圈(环),开始于集合 A 中的无限路径,和开始于集合 B 中的无限路径(在图中通过元素 a 的路径是在两个方向上无限的,所以这个图包含每個类型的一个路径)。一般的说,不可能在有限步骤内判定 A 或 B 的一个给定元素属于那种类型的路径。
上面定义的集合 C 恰好包含了那些开始在 A 中的无限路径所經過的 A 的元素。映射 h 接着被按如下方式定义,对于所有路径它生成一个双射,把在路径中 A 的每个元素,映射到在路径中直接前于或后于它的 B 的一个元素。对于在两个方向上都是无限的路径,和对于有限圈,我们选择映射所有元素到它在路径中的前驱。
最初的证明
康托尔的早先证明有效的依赖于选择公理,通过推导出良序定理的推论。上面给出的证明证实了可以证明这个结果而不使用选择公理。
这个定理也叫做Schroeder-Bernstein定理,但一般會加上康托尔的名字,毕竟他贡献了最初的版本。它也叫做Cantor-Bernstein定理。
引用
- Proofs from THE BOOK, p. 90. ISBN 3540404600