格奥尔格·康托尔
格奥尔格·费迪南德·路德维希·菲利普·康托尔(德語:,1845年3月3日—1918年1月6日),出生于俄国的德国数学家(波羅的海德國人)。他创立了现代集合论,是實數系以至整个微积分理论体系的基础,還提出了势和良序概念的定義;康托爾確定了在兩個集合中的成員,其間一對一關係的重要性,定義了無限且有序的集合,並證明了實數比自然數更多。康托爾對這個定理所使用的證明方法,事實上暗示了“無限的無窮” 的存在。他定義了基數和序數及其算術。康托爾很清楚地自知自覺他的成果,富有極濃厚的哲學興趣。康托爾提出的超越數,最初被當時數學界同儕認為如此反直覺-甚至令人震驚-因而拒絕接受他的理論,且以利奥波德·克罗内克为首的众多数学家长期攻击。克羅內克反對代數數為可數的,而超越數為不可數的證明。
| 格奥尔格·康托尔 Georg Cantor | |
|---|---|
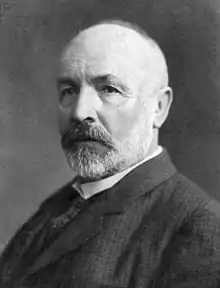 | |
| 出生 | Georg Ferdinand Ludwig Philipp Cantor 1845年3月3日 |
| 逝世 | 1918年1月6日(72歲) |
| 居住地 | |
| 国籍 | 德國 |
| 母校 |
|
| 知名于 | 集合論 |
| 配偶 | Vally Guttmann(1874年结婚) |
| 奖项 | 西爾維斯特獎章(1904年) |
| 科学生涯 | |
| 研究领域 | 數學 |
| 机构 | 哈勒大學 |
| 论文 | De aequationibus secundi gradus indeterminatis(1867) |
| 博士導師 |
|
康托爾本身是一位虔誠的路德派,相信這個理論是經由上帝傳達給他;但一些基督教神學家認為康托爾的理論,是在挑戰神學中只有上帝才具有絕對而唯一的無限性質。康托爾自 1869年任職於德國哈勒大學直到 1918年在哈勒大學附屬精神病院逝世;他的抑鬱症一直再發的病因,被歸咎於當代學界的敵對態度,儘管有人將這些事件解釋為,是他本人所患有的情感雙極障礙的病徵。他所受到的嚴厲攻擊,與後來的讚譽相匹配:在 1904年倫敦皇家學會授予他西爾維斯特獎章,這是皇家學會可授予數學研究者的最高榮譽。
在康托尔死後數十年,維特根斯坦撰文哀悼昔時學術界指責「集合論是假借通過數學而有害處的方言」的氛圍,他認為那是「可笑」和「錯誤」的「完全無稽之談」。当代数学家绝大多数接受康托尔的理论,并认为这是数学史上一次重要的变革。大卫·希尔伯特說:「沒有人能夠把我們從康托爾建立的樂園中趕出去。」(原文另譯:我們屏息敬畏地自知在康托所鋪展的天堂裡,不會遭逢被驅逐出境的。)
生平
青年時期

康托尔1845年出生于俄国圣彼得堡的商人殖民地,並在城裡生活直到他十一歲,他父亲是丹麦商人,母亲是俄国音乐家。他是六個孩子中最年長的一個,被認為是一位傑出的小提琴手。他的祖父弗蘭茲伯姆(Franz Böhm, 1788-1846,小提琴家約瑟夫·伯姆的兄弟)是俄羅斯帝國管弦樂團的著名音樂家和獨奏家。康托爾的父親曾是聖彼得堡證券交易所的成員;當他生病時,為了尋求比聖彼得堡更溫和的冬天,於 1856年他们全家先遷移到了德國的威斯巴登,然後到了法蘭克福。1860年康托爾從達姆施塔特的Realschule區中學畢業;他在數學方面的學業成績優異,尤其是三角學。1862年康托爾進入瑞士聯邦理工學院。在1863年6月他父親去世後,他繼承了豐厚的財產;康托爾將他的學業轉移到柏林大學,研習卡尔·魏尔施特拉斯、利奥波德·克罗内克和恩斯特·库默尔的課程。1866年夏天他在哥廷根大學度過了一段時間。格奧爾格·康托爾是一個好學生,在 1867年于柏林大学获得了博士学位。
任教及研究生涯
康托爾於1867年在柏林大學提交了關於數論的論文。在柏林女子學校短暫講授後,康托爾在哈勒大學任職並在那度過了他整個的職業生涯,在 1869年他任職時所提出的數論論文,因而取得了特许任教资格。1874年康托爾與 Vally Guttmann結婚,在他們度過哈爾茨山脈的蜜月期間,康托爾花了很多時間與理查德·戴德金討論數學,兩人結識是因他兩年前的瑞士度假時而遇到戴德金。他們育有六個孩子,1886年出生的魯道夫是他們最小的孩子。儘管他任教職的薪酬很低,但康托爾能負擔這人口眾多的家庭生計支出,要歸功於他父親的優渥遺產。康托爾在 1872年升任副教授,並在他三十四歲時(1879年)就成為教授,是一個顯著的功名;但康托爾希望在德國柏林更有聲望的領先大學中,擔任主席;然而他的研究工作成果遭遇了太多的反對,每當康托爾在柏林申請更高階的職位,他都被拒絕了。通常是因當時克羅內克有異議的關係,使其所望難以實現。所以康托爾相信因為克羅內克的反對立場,會讓他無法離開哈勒。1881年康托爾的同事愛德華海涅去世,產生了一個主席空缺。哈勒大學採納康托爾的提議,將主席此一職位依序提供給戴德金、安里西·韋伯或是弗朗茨·梅滕斯 這三位,但他們全都拒絕了;這個職位最終任命給 Friedrich Heinrich Albert Wangerin,但他從來沒有接近過康托爾。1882年康托爾和戴德金之間通信聯繫的數學關係告一段落,顯然是由於戴德金拒絕了哈勒大學的主席一職。
在 1884年5月康托爾遭受了自身抑鬱症的第一次發作。對他工作的批評讓他頭腦昏沉:他在 1884年寫給 米塔·列夫勒 的52封信,每封信中都提到克羅內克,其中一段內文揭漏了他自信心所受到的殘害:
......我不知道何時會回到崗位上繼續我的研究。此刻我無能為力,並將我自己限制在論文中最必要的責任上;如果我心智精神能有新鮮的感覺,我能比較快樂地參與學界的活動。
此後康托爾康復,隨後作出了進一步的重要貢獻,包括他的對角論證和定理。1889年康托爾成立了德國數學學會,並於 1891年在哈勒大學主持了首次會議,在那裡他首先介紹了他發明的對角線論證法;儘管克羅內克反對他的工作,但此時他的聲譽已足夠強大到確保當選,為這個學術社群的第一任主席。他最終撇開了克羅內克對他的敵意,並尋求與克羅內克的和解,康托爾邀請他在會上發言,但克羅內克卻因為妻子因當時的滑雪事故中死亡而無法出席。而即使克羅內克在 1891年 12月 29日去世之後,康托爾也再達不到其於 1874-84年發表論文的卓越水準。分裂它們的哲學分歧和困難依舊存在。康托爾在 1897年在瑞士蘇黎世舉行的第一屆國際數學家大會中也發揮了重要作用。
數學領域上的成就
康托爾在 1874至1884 這十年間的研究成果,是集合論的起源。在此之前追溯已往到亞里斯多德時代,數學領域中的集合,從最初就隱含地使用了相當原始的集合概念。沒有人意識到集合這個概念中,有任何未深入研討的內容。在康托爾之前的集合概念,只區分為一般人直覺上容易理解的有限集合,而所謂的“無窮”集合被認為是哲學而非數學研討的命題。康托爾證明無窮集合存在著許多可能的大小,而擴展了數學領域中對於集合概念,其真實涵義的研討。
集合論已經發揮了現代數學基礎理論的作用,因為它明確定義並解釋了,幾乎所有的傳統數學領域(如代數,分析和拓撲)中的數學物件(例如數系和函數)的命題;根據康托爾所建立起的這一套集合理論,提供了標準的公理來證明或反證它們。因此集合論的基本概念,現在被應用在整個數學領域中。在他最早的一篇論文中,康托爾證明了實數系集合和自然數集合,在大小比較上實數系要“多更多了”;這首次表明即使兩個元素都是無窮的集合,在大小上仍然會存在有不同的組合;他也是第一個理解集合論中的一對一對應關係(以下稱為“一一對應關係”)的重要性的人。他用這種概念來定義有限和無窮集合,將後者再區分為可數的(或可數無窮)以及 非可數的無窮集合。
康托爾發展了拓撲中的重要概念,其與基數的關係。例如,他表明康托尔集不是密集的,而與實數系集合一樣具有相同的基數,而有理數的集合是密集而且可數的。他還表明了線性稠密可數的、而沒有終點的序,和有理數集合是同構的。康托爾介紹了集合論的基本結構,如集合的冪集,是對於集合其中所有元素,各種組合而構成的一個子集。他後來證明了即使 屬於無窮集合, 的冪集大小,也將會是嚴格大於 的大小,這個結果很快就被稱為康托爾定理。康托爾發展了整套的集合論和無窮集合的算術,稱為基數和序數,它擴充了自然數的算術。他對基數的標記符號是希伯來文 與自然數下標;對於標示序的符號他採用了希臘字母 ω。這個符號表示法目前數學界仍在使用。
康托爾的連續統假說是 1900年巴黎數學家國際會議,大衛·希爾伯特提出23個尚無證明命題的第一個。康托爾的研究成果也吸引了其它人的關注。美國哲學家皮尔士讚揚他的集合論;而在 1897年蘇黎世舉行的第一屆國際數學家會,康托爾發表的公開講座之後,Hurwitz 和阿达马也都表示了欽佩。在那次大會上康托爾重新與戴德金交換了友誼和信件。自 1905年起康托爾與英國翻譯家菲利普朱爾丹就集合論的歷史,和康托爾的宗教思想,進行了對談,這些對談後來集成出版為康托爾的講述作品。
數論,三角級數和序數
康托爾的前十篇論文題目是關於數論。在哈勒大學教授愛德華海涅的建議下,康托轉向分析。海涅提出了困惑著約翰·彼得·古斯塔夫·勒熱納·狄利克雷、鲁道夫·利普希茨、波恩哈德·黎曼和海涅自己的問題:如何呈現三角级数的建構函數的唯一性質?康托爾在 1869年解決了這個難題,而在研究這個三角級數唯一定理的時候,他發現了超限序數,出現在對於三角級數的集合S,其下標為n的第n個索引的導出集合 Sn之中。
1870 至 1872年之間康托爾發表了更多關於三角函數的論文,並且還將無理數定義為有理數的收斂序列。戴德金引用了這篇論文,並在他的論文中首次提出了戴德金切割的實數定義。即使康托爾革命性地以無限基數的概念來擴大集合概念的同時,他卻自相矛盾地反對同期數學分析學者 Otto Stolz 和 Paul du Bois-Reymond 的無限小理論;康托爾還發表了一個錯誤的“證明”,試圖證明無窮小量的不一致性。
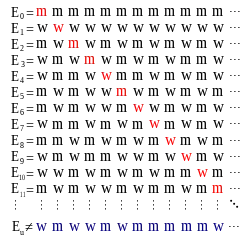
一一对应和對角線證明方法
康托尔提出了通过一一对应的方法对无限集合的大小进行比较,并将能够彼此建立一一对应的集合称为等势,即可以被认为是“一样大”的。他引入了可数无穷的概念,用来指与自然数集合等势的集合,并证明了有理数集合是可数无穷,而实数集合不是可数无穷,这表明无穷集合的确存在着不同的大小,他称与实数等势(从而不是可数无穷)的集合为不可数无穷。原始证明发表于 1874年,这个证明使用了较为复杂的归纳反证法。1891年他用对角线法重新证明了这个定理。另外,他证明了代数数集合是可数集,以及 维空间与一维空间之间存在一一对应。在上述理论的基础上,康托尔又系统地研究了序数理论,提出了良序定理,即可以给任何集合内的所有元素定义一个大小关系,使得任意两个元素都可以比较大小,且该集合的任意子集都有最小元素。
哲學,宗教和康托爾的數學