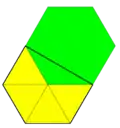
扭稜截半六邊形鑲嵌
在幾何學中,扭稜截半六邊形鑲嵌是歐幾里德平面上截半六邊形鑲嵌的一種變形,是種平面鑲嵌,屬於不均勻半正鑲嵌的一種,它有兩種頂點,其中一個是四個三角形和一個六邊形的公共頂點;另一個是六個三角形的公共頂點。在施萊夫利符號中用st1{6,3}來表示。 該鑲嵌屬於複合正多邊形密鋪[2],是一種由二種正多邊形組成的不均勻半正鑲嵌圖,該鑲嵌圖是由正三角形和正六邊形組成。
 | |||
| 類別 | 不均勻半正鑲嵌 | ||
|---|---|---|---|
| 對偶多面體 | 花形五邊形-三六邊形鑲嵌 | ||
| 數學表示法 | |||
| 施萊夫利符號 | st1{6,3} | ||
| 組成與佈局 | |||
| 頂點圖 | (1/2)(36) + (1/2)(34,6)[1] | ||
| 對稱性 | |||
| 對稱群 | p6, [6,3]+, (632) | ||
| 旋轉對稱群 | p6, [6,3]+, (632) | ||
| 圖像 | |||
| |||
相關多面體與鑲嵌
| 对称性: [6,3], (*632) | [6,3]+, (632) | [1+,6,3], (*333) | [6,3+], (3*3) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| {6,3} | t0,1{6,3} | t1{6,3} | t1,2{6,3} | t2{6,3} | t0,2{6,3} | t0,1,2{6,3} | s{6,3} | h{6,3} | h1,2{6,3} | |
| 半正对偶 | ||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 | ||
| V6.6.6 | V3.12.12 | V3.6.3.6 | V6.6.6 | V3.3.3.3.3.3 | V3.4.12.4 | V.4.6.12 | V3.3.3.3.6 | V3.3.3.3.3.3 | ||
參見
參考文獻
- Grünbaum, Branko; and Shephard, G. C. . New York: W. H. Freeman. 1987. ISBN 0-7167-1193-1.
- 《圖解數學辭典》天下遠見出版 複合正多邊形密鋪 ISBN 986-417-614-5
- Krötenheerdt, O. "Die homogenen Mosaike n-ter Ordnung in der euklidischen Ebene. I." Wiss. Z. Martin-Luther-Univ. Halle-Wittenberg, Math.-Natur. Reihe 18, 273-290, 1969.
- Grünbaum, B. and Shephard, G. C. Tilings and Patterns. New York: W. H. Freeman, 1986.
- 埃里克·韦斯坦因. . MathWorld.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
- Grünbaum, Branko ; and Shephard, G. C. . New York: W. H. Freeman. 1987. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p.58-65)
- Williams, Robert. . Dover Publications, Inc. 1979. ISBN 0-486-23729-X. p.39
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.