射影定理
射影定理(台灣稱「母子相似定理」)(英語:),又稱歐幾里得定理(英語:),是平面幾何中的一個定理。這個定理指出,在一個直角三角形中,一條直角邊的平方,相等於三角形的斜邊乘以該直角邊在斜邊上的正投影。[1]這個定理出現在歐幾里得所著《幾何原本》第一卷當中,是第 47 個命題畢氏定理證明過程的一部分。[2]
定理內容
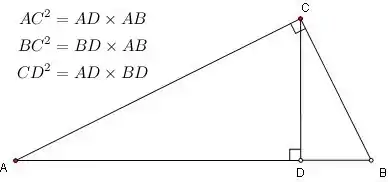
在 ΔABC 中,∠C = 90°,以及 CD ⊥ AB。AD 及 BD 分別是 AC 及 BC 在底邊 AB 的正投影。
在 ΔABC 中,∠C = 90°。設 CD 在 AB 的上的高,則有:
在這裡,AD 及 BD 分別是 AC 及 BC 在底邊 AB 的正投影,故定理以此為名。
相關定理
一般三角形的情況
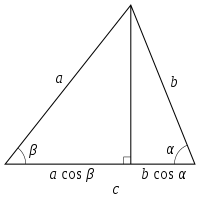
邊長 a 及 b 在底邊 c 的正投影,分別是 a cos β 及 b cos α。
對於 ∠C ≠ 90° 的情況,三角形邊長的正投影可用餘弦求得:
以上結果從餘弦的定義直接可得。
把上面兩式相加,即可得:
以上公式,又被稱為「第一餘弦定理」。[4]然而,一般「餘弦定理」所指的,是另一條定理(「第二餘弦定理」),詳見餘弦定理。
三維空間上的推廣
三直角四面體
.svg.png.webp)
一個四面體。若構成頂點的三個面角皆為直角,則這是一個三直角四面體。
射影定理在三維空間上,也有相應的推廣。設三直角四面體 ABCD 中,∠ADB = ∠ADC = ∠BDC = 90°。又設 D 在斜面 ΔABC 的正投影為 E。我們則有:
其中 [ΔABC] 表示 ΔABC 的面積。
把以上三條等式相加,則可得德古阿定理:
一般四面體
在四面體 ABCD 中,設 ΔABC 為底面。又設 D 在 ΔABC 的正投影為 E。我們則有:
其中 α 、β 及 γ 分別是 AD 、BD 及 CD 與底面 ΔABC 的夾角。
另外亦有:
其中 θ 、ϕ 及 ψ 分別是 ΔABD 、ΔACD 及 ΔBCD 與底面 ΔABC 的夾角。
將上面三條等式相加,可得:
是上面提到「第一餘弦定理」的三維推廣。
任意圖形的投影
更進一步地說,面積為 S 的任意平面圖形,在底面的正投影的面積 Sproj,都可用餘弦求得:
其中 θ 是該平面圖形與底面的夾角。
參考資料
- 曹才翰 主編; 沈復興, 孫瑞清, 餘炯沛等 副編. . 瀋陽出版社. 1991. ISBN 9787805564241.
- Euclid. . c 300 BC [2020-02-15]. (原始内容存档于2021-02-24).
- Euclid. . c 300 BC [2020-02-15]. (原始内容存档于2020-02-03).
- 中原晴彦. (PDF). 順天サイエンスライブラリー. 2003 [2020-02-15]. (原始内容存档 (PDF)于2020-02-15).
- Sergio A. Alvarez. (PDF). Center for Nonlinear Analysis and Department of Mathematical Sciences, Carnegie Mellon University. [2020-02-15]. (原始内容存档 (PDF)于2012-10-02).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.