拉普拉斯方法

在数学上，以皮埃尔-西蒙·拉普拉斯命名的拉普拉斯方法是用于得出下列积分形式的近似解的方法：

\int _{a}^{b}\!e^{Mf(x)}\,dx

其中的 ƒ(x) 是一個二次可微函数， M 是一個很大的數，而積分邊界點 a 與 b 則允許為無限大。此外，函數 ƒ(x) 在此積分範圍內的全域極大值所在處必須是唯一的並且不在邊界點上。則它的近似解可以寫為:

\int _{a}^{b}\!e^{Mf(x)}\,dx\approx {\sqrt {\frac {2\pi }{M\left|f''(x_{0})\right|}}}e^{Mf(x_{0})}{\text{ as }}M\to \infty .\,

其中的 x₀ 為極大值所在處。這方法最早是拉普拉斯在 (1774, pp. 366–367) 所發表。(待考查)

拉普拉斯方法的想法概論

1. 相對誤差

首先，我們得先知道的是，這裡所謂的近似解是以相對誤差在講，而不是指絕對誤差。因此，令

$s={\sqrt {\frac {2\pi }{M\left|f''(x_{0})\right|}}}$ ，

此 s 很顯然的當 M 很大時為一個微小的數，則上述的積分可以寫為

{\begin{aligned}\int _{a}^{b}\!e^{Mf(x)}\,dx&=se^{Mf(x_{0})}{\frac {1}{s}}\int _{a}^{b}\!e^{M(f(x)-f(x_{0}))}\,dx\\&=se^{Mf(x_{0})}\int _{(a-x_{0})/s}^{(b-x_{0})/s}\!e^{M(f(sy+x_{0})-f(x_{0}))}\,dy\end{aligned}}

因此，我們的相對誤差很顯然的為

\left|\int _{(a-x_{0})/s}^{(b-x_{0})/s}e^{M(f(sy+x_{0})-f(x_{0}))}dy-1\right|

現在，讓我們把積分分為 $y\in [-D_{y},D_{y}]$ 的與餘下的部分。

2. 函數

e^{M\left(f(sy+x_{0})-f(x_{0})\right)}

在極大值附近的行為，當

M

很大時會趨近於

e^{-\pi y^{2}}

我们现在来研究 $M\left(f(x)-f(x_{0})\right)$ 的泰勒展開。這裡展開的原點取 x₀ ，並將變數由 x 換為 y 因為我們是在對 y 做積分，再加上 x₀ 為函數極大值所在處，因此，

{\begin{aligned}M\left(f(x)-f(x_{0})\right)&={\frac {Mf''(x_{0})}{2}}s^{2}y^{2}+{\frac {Mf'''(x_{0})}{6}}s^{3}y^{3}+\cdots \\&=-\pi y^{2}+O\left({\frac {1}{\sqrt {M}}}\right).\end{aligned}}

會發現高於二次微分的部分當 M 增大時，會被壓抑掉，而此指數函數則會越來越接近高斯函數 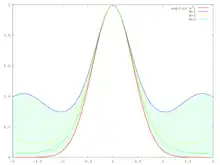$e^{-\pi y^{2}}$ 且 $\int _{-\infty }^{\infty }e^{-\pi y^{2}}dy=1$ 。如下圖所示：

圖為

e^{M[f(sy+x_{0})-f(x_{0})]}

，其中M為 1, 2 與 3。紅色線為

e^{-\pi y^{2}}

3. 當

M

增加，則相對應的

x

範圍變小

 $y\in [-D_{y},D_{y}]$  的部分由上面論述可知當 M 越大則越接近高斯函數；並且有趣的是，相對應的 x 區間則越來越小，因為   $x\in [-sD_{y},sD_{y}]$  與  ${\sqrt {M}}$  成反比。

4.若拉普拉斯方法所用的積分會收斂，它的相對誤差相對應的非極大值附近的其餘部分的積分就會隨

M

增大而趨近於0

所以，即便 D_y 取非常大， sD_y 最後還是會變得非常小，那麼，我們怎麼保證餘下的部分的積分也會趨近到0？

簡單的想法是，設法找一個函數 $m(x)$ ，使它在餘下的區域內 $m(x)\geq f(x)$ ，並且隨著 $M$ 的增大， $e^{Mm(x)}$ 的積分會趨近於0 即可。而指數函數只要指數部分為實數，它就一定大於0，並且當指數變大時，指數函數也會跟著變大。基於這兩個理由， $e^{Mf(x)}$ 的積分也會趨近於0。在此，我們可以選擇此 $m(x)$ 為過 $x=sD_{y}$ 的切線函數，如下圖所示：

m(x)

以斜直線代表，為通過位於

x=sD_{y}+x_{0}

的切線，當

sD_{y}

越小，涵蓋的範圍越大

若為有限積分區間，我們可以看出，只要 $M$ 夠大，這切線的斜率就會趨近於0 ，因此，不管 $f(x)$ 在其餘部分是否連續，它們總會在這切線以下，並且很容易證明(後面會證) $e^{Mm(x)}$ 的積分當 $M$ 很大時，就會趨近於0。

然而，若積分範圍是無限大的話，那麼， $m(x)$ 就有可能總是與 $f(x)$ 有相交，若有相交，則表示無法保證 $e^{Mf(x)}$ 的積分最後會趨近於0。比方 $f(x)={\frac {sin(x)}{x}}$ 的情形下，不管 $M$ 為多少，它的 $\int _{0}^{\infty }e^{Mf(x)}dx$ 總是會發散。所以，對於積分範圍為無限大的情形，還得要求 $\int _{d}^{\infty }e^{Mf(x)}dx$ 會收斂才行，那麼，只要 $d$ 越來越大，該積分就會趨近於0。而這 $d$ 可選為 $m(x)$ 與 $f(x)$ 相交之處即可，即保證所有餘下的部分的積分會趨近於0。

也許您會問說，為何不是要求 $\int _{d}^{\infty }e^{f(x)}dx$ 會收斂？舉個例子，若 $f(x)$ 在餘下區域內為 $-\ln x$ ，則 $e^{f(x)}={\frac {1}{x}}$ ，積分會發散，然而，當 $M=2$ ， $e^{Mf(x)}={\frac {1}{x^{2}}}$ 的積分卻是收斂的。所以，有的函數在 $M$ 小的時候會發散，然而，當 $M$ 夠大時卻會是收斂的。

基於上述四點，就有辦法證明拉普拉斯方法的可靠性。而 Fog(2008) 又將此方法推廣到任意精確。 ***待考查***

此方法的正式表述與證明：

假設 $f(x)$ 是一個在 $x_{0}\in (a,b)$ 這點滿足 (1) $f(x_{0})=\max _{[a,b]}f(x)$ ，(2)唯一全域最大，(3) $x_{0}$ 附近為二階可微且 $f''(x_{0})<0$ (4) 當拉普拉斯方法的積分範圍為無限大時，此積分會收斂，

則，

\lim _{n\to +\infty }\left({\frac {\int _{a}^{b}e^{nf(x)}\,dx}{\left(e^{nf(x_{0})}{\sqrt {\frac {2\pi }{n(-f''(x_{0}))}}}\right)}}\right)=1

證明：

下限：

在 $f''$ 要求連續的條件底下，給定任意大於0的 $\varepsilon$ 就能找到一個 $\delta >0$ 使得在 $|x_{0}-x|<\delta$ 這區間內所有的 $f''(x)\geq f''(x_{0})-\varepsilon .$ 。由泰勒展開我們可以得知，在 $x\in (x_{0}-\delta ,x_{0}+\delta )$ 區間內， $f(x)\geq f(x_{0})+{\frac {1}{2}}(f''(x_{0})-\varepsilon )(x-x_{0})^{2}$ 。

這樣，我們就得到本方法的積分下限了：

\int _{a}^{b}e^{nf(x)}\,dx\geq \int _{x_{0}-\delta }^{x_{0}+\delta }e^{nf(x)}\,dx\geq e^{nf(x_{0})}\int _{x_{0}-\delta }^{x_{0}+\delta }e^{{\frac {n}{2}}(f''(x_{0})-\varepsilon )(x-x_{0})^{2}}\,dx=e^{nf(x_{0})}{\sqrt {\frac {1}{n(-f''(x_{0})+\varepsilon )}}}\int _{-\delta {\sqrt {n(-f''(x_{0})+\varepsilon )}}}^{\delta {\sqrt {n(-f''(x_{0})+\varepsilon )}}}e^{-{\frac {1}{2}}y^{2}}\,dy

其中最後一個等號來自於變數變換： $y={\sqrt {n(-f''(x_{0})+\varepsilon )}}(x-x_{0})$ 。請記得 $f''(x_{0})<0$ ，所以我們才會對它的負號取開根號。

接著讓我們對上面的不等式兩邊同除以 $e^{nf(x_{0})}{\sqrt {\frac {2\pi }{n(-f''(x_{0}))}}}$ 並且對 $n$ 取極限，則

\lim _{n\to +\infty }\left({\frac {\int _{a}^{b}e^{nf(x)}\,dx}{\left(e^{nf(x_{0})}{\sqrt {\frac {2\pi }{n(-f''(x_{0}))}}}\right)}}\right)\geq \lim _{n\to +\infty }{\frac {1}{\sqrt {2\pi }}}\int _{-\delta {\sqrt {n(-f''(x_{0})+\varepsilon )}}}^{\delta {\sqrt {n(-f''(x_{0})+\varepsilon )}}}e^{-{\frac {1}{2}}y^{2}}\,dy{\sqrt {\frac {-f''(x_{0})}{-f''(x_{0})+\varepsilon }}}={\sqrt {\frac {-f''(x_{0})}{-f''(x_{0})+\varepsilon }}}

既然上式是對任意大於0的 $\varepsilon$ 都對，所以我們得到：

\lim _{n\to +\infty }\left({\frac {\int _{a}^{b}e^{nf(x)}\,dx}{\left(e^{nf(x_{0})}{\sqrt {\frac {2\pi }{n(-f''(x_{0}))}}}\right)}}\right)\geq 1

請注意，上面的證明也適用於 $a=-\infty$ 或 $b=\infty$ 或雙雙跑到正負無限大的情況

上限：

證明上限的部分其實和證明下限的部分很像，但是會較麻煩。再一次，我們取 $\varepsilon >0$ ，不過，不再是任意而是多了一個要求 $\varepsilon$ 得夠小以致於 $f''(x_{0})+\varepsilon <0$ 。接著，就如同之前的證明，因著 $f''$ 被要求連續，並且根據泰勒定理我們會發現總存在一個 $\delta >0$ 以至於在 $|x-x_{0}|<\delta$ 區間裡， $f(x)\leq f(x_{0})+{\frac {1}{2}}(f''(x_{0})+\varepsilon )(x-x_{0})^{2}$ 總是可以成立。最後，在我們的假設裡 (假設 $a,b$ 都是有限值) ，由於 $x_{0}$ 是全域最大所在處，我們總可以找到一個 $\eta >0$ 使得所有在 $|x-x_{0}|\geq \delta$ 這區間裡， $f(x)\leq f(x_{0})-\eta$ 總是成立。

現在，萬事俱備，東風就在下面啦：

\int _{a}^{b}e^{nf(x)}\,dx\leq \int _{a}^{x_{0}-\delta }e^{nf(x)}\,dx+\int _{x_{0}-\delta }^{x_{0}+\delta }e^{nf(x)}\,dx+\int _{x_{0}+\delta }^{b}e^{nf(x)}\,dx\leq (b-a)e^{n(f(x_{0})-\eta )}+\int _{x_{0}-\delta }^{x_{0}+\delta }e^{nf(x)}\,dx

\leq (b-a)e^{n(f(x_{0})-\eta )}+e^{nf(x_{0})}\int _{x_{0}-\delta }^{x_{0}+\delta }e^{{\frac {n}{2}}(f''(x_{0})+\varepsilon )(x-x_{0})^{2}}\,dx\leq (b-a)e^{n(f(x_{0})-\eta )}+e^{nf(x_{0})}\int _{-\infty }^{+\infty }e^{{\frac {n}{2}}(f''(x_{0})+\varepsilon )(x-x_{0})^{2}}\,dx

\leq (b-a)e^{n(f(x_{0})-\eta )}+e^{nf(x_{0})}{\sqrt {\frac {2\pi }{n(-f''(x_{0})-\varepsilon )}}}

如果我們對上面的不等式兩邊皆除以 $e^{nf(x_{0})}{\sqrt {\frac {2\pi }{n(-f''(x_{0}))}}}$ 並且順便取極限的話，會得到：

\lim _{n\to +\infty }\left({\frac {\int _{a}^{b}e^{nf(x)}\,dx}{\left(e^{nf(x_{0})}{\sqrt {\frac {2\pi }{n(-f''(x_{0}))}}}\right)}}\right)\leq \lim _{n\to +\infty }\left((b-a)e^{-\eta n}{\sqrt {\frac {n(-f''(x_{0}))}{2\pi }}}+{\sqrt {\frac {-f''(x_{0})}{-f''(x_{0})-\varepsilon }}}\right)={\sqrt {\frac {-f''(x_{0})}{-f''(x_{0})-\varepsilon }}}

再一次，因為 $\varepsilon$ 可以取任意大於0的值，所以我們得到了上限了：

\lim _{n\to +\infty }\left({\frac {\int _{a}^{b}e^{nf(x)}\,dx}{\left(e^{nf(x_{0})}{\sqrt {\frac {2\pi }{n(-f''(x_{0}))}}}\right)}}\right)\leq 1

把上限與下限兩個證明同時考慮，整個證明就完成了。

注意，關於上限的證明，很明顯的當我們把它應用在 $a$ 或 $b$ 為正負無限大時，該上限證明會失敗。那怎麼辦呢？我們需要再多假設一些東西。一個充分但非必要的假設是：當 $n=1$ 時，此積分 $\int _{a}^{b}e^{nf(x)}\,dx$ 為有限值，並且上面所說的 $\eta$ 是存在的 (注意，當 $[a,b]$ 區間是無限的時候，這假設是必要的) 。整個證明過程就如同先前所顯示的那樣，只不過下列的積分部分要做點改變：

\int _{a}^{x_{0}-\delta }e^{nf(x)}\,dx+\int _{x_{0}+\delta }^{b}e^{nf(x)}\,dx

必須利用上述的假設，而改為：

\int _{a}^{x_{0}-\delta }e^{nf(x)}\,dx+\int _{x_{0}+\delta }^{b}e^{nf(x)}\,dx\leq \int _{a}^{b}e^{f(x)}e^{(n-1)(f(x_{0})-\eta )}\,dx=e^{(n-1)(f(x_{0})-\eta )}\int _{a}^{b}e^{f(x)}\,dx

以取代先前會得到的 $(b-a)e^{n(f(x_{0})-\eta )}$ ，這樣的話，當我們除以 $e^{nf(x_{0})}{\sqrt {\frac {2\pi }{n(-f''(x_{0}))}}}$ ，就會改得到如下的結果：

{\frac {e^{(n-1)(f(x_{0})-\eta )}\int _{a}^{b}e^{f(x)}\,dx}{e^{nf(x_{0})}{\sqrt {\frac {2\pi }{n(-f''(x_{0}))}}}}}=e^{-(n-1)\eta }{\sqrt {n}}e^{-f(x_{0})}\int _{a}^{b}e^{f(x)}\,dx{\sqrt {\frac {-f''(x_{0})}{2\pi }}}

這樣的話，當我們取 $n\rightarrow \infty$ 時，上式的值就會趨近於 $0$ 。而剩下的部分的證明就還是如同原先的證明，不做改變。

再強調一次，這裡我們多加給無限大積分範圍的情形的條件，是充分，但非必要。不過，這樣的條件已經可以適用在許多情形了(但非全部)。這考慮條件簡單來講就是積分區間得是被良好定義的(即不能是無限大的)，並且被積函數在 $x_{0}$ 必須是真的極大 (意即 $\eta >0$ 必須真的存在) ；如果這積分區間是無限大的話，要求 $n=1$ 時的此拉普拉斯方法所用的積分值要為有限並非必要的，其實只要當 $n$ 大於某數時，此積分值會是有限的即可。

其他形式

有時拉普拉斯方法也會被寫成其他形式，如：

\int _{a}^{b}\!h(x)e^{Mg(x)}\,dx\approx {\sqrt {\frac {2\pi }{M|g''(x_{0})|}}}h(x_{0})e^{Mg(x_{0})}{\text{ as }}M\to \infty \,

其中 $h$ 為正 (好像不必要)。

重要的是，這方法精確度與函數 $g(x)$ 和 $h(x)$ 有關。 [1] ***待考查***

相對誤差的推導

首先，由於極大值所在設為 $x_{0}=0$ 並不影響計算結果，所以以下的推導皆如此假設。此外，我們想要的是相對誤差 $\left|R\right|$ ，所以

\int _{a}^{b}\!h(x)e^{Mg(x)}\,dx=h(0)e^{Mg(0)}s\underbrace {\int _{a/s}^{b/s}{\frac {h(x)}{h(0)}}e^{M\left[g(sy)-g(0)\right]}dy} _{1+R}

其中 $s\equiv {\sqrt {\frac {2\pi }{M\left|g''(0)\right|}}}$ ，所以，若我們令 $A\equiv {\frac {h(sy)}{h(0)}}e^{M\left[g(sy)-g(0)\right]}$ 且 $A_{0}\equiv e^{-\pi y^{2}}$ ，則

\left|R\right|=\left|\int _{a/s}^{b/s}A\,dy-\int _{-\infty }^{\infty }A_{0}\,dy\right|

所以，只要我們求得上式的上限為何，即可得相對誤差。注意，這裡的推導還可以再優化，不過，由於此處我只想顯示它會收斂到0，因此，不再細推。

由於 $\left|A+B\right|\leq |A|+|B|$ ，因此

|R|<\underbrace {\left|\int _{D_{y}}^{\infty }A_{0}dy\right|} _{(a_{1})}+\underbrace {\left|\int _{D_{y}}^{b/s}Ady\right|} _{(b_{1})}+\underbrace {\left|\int _{-D_{y}}^{D_{y}}\left(A-A_{0}\right)dy\right|} _{(c)}+\underbrace {\left|\int _{a/s}^{-D_{y}}Ady\right|} _{(b_{2})}+\underbrace {\left|\int _{-\infty }^{-D_{y}}A_{0}dy\right|} _{(a_{2})}

其中 $(a_{1})$ 與 $(a_{2})$ 雷同，所以只算 $(a_{1})$ ，經過 $z\equiv \pi y^{2}$ 的變換後，得到

(a_{1})=\left|{\frac {1}{2{\sqrt {\pi }}}}\int _{\pi D_{y}^{2}}^{\infty }e^{-z}z^{-1/2}dz\right|<{\frac {e^{-\pi D_{y}^{2}}}{2\pi D_{y}}}

也就是說，只要 $D_{y}$ 取得夠大，它就會趨近於0。

而 $(b_{1})$ 與 $(b_{2})$ 也雷同，所以也只算一個：

(b_{1})\leq \left|\int _{D_{y}}^{b/s}\left[{\frac {h(sy)}{h(0)}}\right]_{\text{max}}e^{Mm(sy)}dy\right|

其中

m(x)\geq {\frac {1}{M}}\ln {\frac {h(x)}{h(0)}}+g(x)-g(0)\,\,{\text{as}}\,\,x\in [sD_{y},b]

並且 $h(x)$ 在此範圍內要與 $h(0)$ 同號。這裡讓我們選過 $x=sD_{y}$ 的切線為 $m(x)$ 吧！即 $m(sy)=g(sD_{y})-g(0)+g'(sD_{y})\left(sy-sD_{y}\right)$ ，如圖所示：

m(x)

以斜直線代表，為通過位於

x=sD_{y}

的切線

由圖可以看出，當 $s$ 或者 $D_{y}$ 變小時，滿足上列不等式的區間會變大，因此，為了涵蓋整個區間， $D_{y}$ 有了上限。此外， $e^{-\alpha x}$ 的積分也相對容易，因此，很適合用來預估誤差。

由泰勒展開我們得知，

{\begin{aligned}M\left[g(sD_{y})-g(0)\right]&=M\left[{\frac {g''(0)}{2}}s^{2}D_{y}^{2}+{\frac {g'''(\xi )}{6}}s^{3}D_{y}^{3}\right]\,\,{\text{as}}\,\,\xi \in [0,sD_{y}]\\&=-\pi D_{y}^{2}+{\frac {(2\pi )^{3/2}g'''(\xi )D_{y}^{3}}{6{\sqrt {M}}|g''(0)|^{3/2}}},\end{aligned}}

且

{\begin{aligned}Msg'(sD_{y})&=Ms\left(g''(0)sD_{y}+{\frac {g'''(\zeta )}{2}}s^{2}D_{y}^{2}\right),\,\,{\text{as}}\,\,\zeta \in [0,sD_{y}]\\&=-2\pi D_{y}+{\sqrt {\frac {2}{M}}}\left({\frac {\pi }{|g''(0)|}}\right)^{3/2}g'''(\zeta )D_{y}^{2}\end{aligned}}

然後將它們代回 $(b_{1})$ 的計算裡，不過，您可以看到，上述的兩個餘項皆與 $M$ 的開根號成反比，為了式子的漂亮，讓我省略它們吧！不省略只是看起來較醜陋而已，不過，那樣子較嚴謹便是。

{\begin{aligned}(b_{1})&\leq \left|\left[{\frac {h(sy)}{h(0)}}\right]_{\text{max}}e^{-\pi D_{y}^{2}}\int _{0}^{b/s-D_{y}}e^{-2\pi D_{y}y}dy\right|\\&\leq \left|\left[{\frac {h(sy)}{h(0)}}\right]_{\text{max}}e^{-\pi D_{y}^{2}}{\frac {1}{2\pi D_{y}}}\right|.\end{aligned}}

所以，原則上也是 $D_{y}$ 越大則越趨近於0。只不過，在決定 $m(x)$ 的過程，設下了 $D_{y}$ 的上限。

至於靠近極大值的點的積分，我們一樣可以利用泰勒展開來求，當 $h(x)$ 在此點的一階微分不為0時，

{\begin{aligned}(c)&\leq \int _{-D_{y}}^{D_{y}}e^{-\pi y^{2}}\left|{\frac {sh'(\xi )}{h(0)}}y\right|\,dy\\&<{\sqrt {\frac {2}{\pi M|g''(0)|}}}\left|{\frac {h'(\xi )}{h(0)}}y\right|_{\text{max}}\left(1-e^{-\pi D_{y}^{2}}\right)\end{aligned}}

會看到它原則上與 $M$ 的開根號成反比，其實，當 $h(x)$ 為常數時，積分出來的也會有如此的行為。

所以，概括的講，靠近極大點的附近的積分原則上會隨著 ${\sqrt {M}}$ 的增大而變小，而其餘的部分，只要 $D_{y}$ 夠大，也會趨近於0，只是這 $D_{y}$ 是有上限的，取決於我們所找的上限函數 $m(x)$ 是否在這區間內總是大於 $g(x)-g(0)$ ；不過，一旦有一個滿足條件的 $m(x)$ 被找到，由於切線的起點為 $x=sD_{y}$ ，因此， $D_{y}$ 可以取正比於 ${\sqrt {M}}$ 即可，所以， $M$ 越大， $D_{y}$ 也可以設越大。

至於多維的情形，讓我們令 $\mathbf {x}$ 是一個 $n$ 維向量，而 $f(\mathbf {x} )$ 則是一個純量函數，則此拉普拉斯方法可以寫成

\int e^{Mf(\mathbf {x} )}\,d^{n}x\approx \left({\frac {2\pi }{M}}\right)^{n/2}|-H(f)(\mathbf {x} _{0})|^{-1/2}e^{Mf(\mathbf {x} _{0})}{\text{ as }}M\to \infty \,

其中的 $H(f)(\mathbf {x} _{0})$ 是一個在 $\mathbf {x} _{0}$ 取值的海森矩陣，而 $|\cdot |$ 則是指矩陣的行列式；此外，與單變數的拉普拉斯方法類似，這裡的海森矩陣必須為負定矩陣，即該矩陣的所有本徵值皆小於0，這樣才會是極大值所在。.[2]

拉普拉斯方法的推廣：最速下降法

此拉普拉斯方法可以被推廣到複分析裡頭使用，搭配留數定理，以找出一個過最速下降點的 contour (翻路徑的話，會與path integral 相衝，所以，這裡還是以英文原字稱呼) 的曲線積分，用來取代原有的複數空間的 contour積分。因為有時 $f(z)$ 的一階微分為0的點未必就在實數軸上，而就算真在實數軸上，也未必二階微分在 $x$ 方向上為小於0 的實數；此種情況下，就得使用最速下降法了。由於最速下降法中，已經利用另一條通過最速下降的鞍點來取代原有的 contour 積分，經過變數變換後就會變得有如拉普拉斯方法，因此，我們可以透過這新的 contour ，找到原本的積分的漸進近似解，而這將大大的簡化整個計算。就好像原本的路徑像是在蜿蜒的山路開車，而新的路徑就像乾脆繞過這座山開，反正目的只是到達目的地而已，留數定理已經幫我們把中間的差都算好了。請讀 Erdelyi (2012)與 Arfken & Weber (2005) 的書裡有關 steepest descents 的章節。

以下就是該方法在z 平面下的形式：

\int _{a}^{b}\!e^{Mf(z)}\,dz\approx {\sqrt {\frac {2\pi }{-Mf''(z_{0})}}}e^{Mf(z_{0})}{\text{ as }}M\to \infty .\,

其中 z₀ 就是新的路徑通過的鞍點。注意，開根號裡的負號是用來指定最速下降的方向，千萬別認為取 $f''(z_{0})$ 的絕對值來取代這個負號，若然，那就大錯特錯了。另外要注意的是，如果該被積函數是，就有必要將被新舊 contour 包到的極點所貢獻的留數給加入，範例請參考 Okounkov 的文章 arXiv:math/0309074 的第三章。

更進一步一般化

最速下降法還可以更進一步的推廣到所謂的 非線性穩定相位/最速下降法 (nonlinear stationary phase/steepest descent method)。這方法主要用在解非線性偏微分方程，透過將非線性偏微分方程轉換為求解柯西變換(Cauchy transform)的積分形式，就可以藉由最速下降法的想法來得到非線性解的漸進解。

以艾里方程(線性) $y''=xy$ 為例，它可以寫成積分形式如下：

y_{j}(x)={\frac {1}{2\pi i}}\int _{\gamma _{j}}e^{{\frac {1}{3}}t^{3}-xt}dt

由這條積分式，我們就可以藉由最速下降法(若 $\gamma _{j}$ 指的是負實數軸，那麼就回到此拉普拉斯方法了)來得到它的漸進解了。

然而，若方程式如 KdV方程 $y_{t}+6yy_{x}+y_{xxx}=0$ 是個非線性偏微分方程，想要找到它的解相對應的一個複數 contour 積分的話，就沒那麼簡單，在非線性穩定相位/最速下降法裡所用到的概念主要是基於散射逆轉換 (inverse scattering transform) 的處理方式，即先將原本的非線性偏微分方程變成 Lax 對，其中一個像是線性的薛丁格方程式，其位能障為我們要找的 $y$ ，本徵值為 $\lambda$ ，波函數為 $\phi _{\lambda }$ (不過，它並非我們所要的 $y$ )；因此可以解它的散射矩陣，若利用解析延拓將原本的波函數由實數 $\lambda$ 延拓到複數空間時，就可以得到黎曼希爾伯特問題(RHP)的形式。利用這個黎曼希爾伯特問題(RHP) ，我們可以解得 $\phi$ 的柯西變換的積分形式，再利用此線性薛丁格方程的特性，就可以反推出 $y$ 的複數 contour 積分形式了。

而 Lax 對的另一個偏微分方程則是決定每個 $\phi _{\lambda }$ 隨時間變化的行為，由於 $y$ 在 $x\rightarrow \pm \infty$ 時被要求為0 ，會發現整個偏微分方程會變得十分簡單，並且只決定 $c(\lambda ,t)\phi _{\lambda }$ 裡的 $c(\lambda ,t)$ 的值，不過，條件是 $\phi _{\lambda }$ 必須是指由正負無限遠入射或反射波的解。這樣，我們所得到的這個只與時間與本徵值有關的係數 $c(\lambda ,t)$ 就可以直接被應用在上述的黎曼希爾伯特問題(RHP)裡的躍變矩陣裡了。

接著就是非線性穩定相位/最速下降法所要做的工作，即找出鞍點來，在該點附近基於最速下降法的精神做近似。不過，這近似因著考慮到收斂性，需要將原本的 contour 變形，與將原本的黎曼希爾伯特問題(RHP)作轉換，所以有再比原本的最速下降法多出一些步驟來。

這整個方法最早由 Deift 與 Zhou 在 1993 基於 Its 之前的工作所提出的，後續又有許多人加以改進，主要的應用則有孤波理論，可積模型等。

複數積分

以下的積分常用在拉普拉斯變換#拉普拉斯逆變換裡，

{\frac {1}{2\pi i}}\int _{c-i\infty }^{c+i\infty }g(s)e^{st}\,ds

假定我們想要得到該積分在 $t>>1$ 時的結果(若 $t$ 為時間，通常就是在找經過夠久時間後達穩定的結果)，我們可以透過解析延拓的概念，先將這時間換成虛數，如 t = iu 並且一併做 $s=c+ix$ 的變換，則我們可以將上式轉換為如下的拉普拉斯變換#雙邊拉普拉斯變換

{\frac {1}{2\pi }}\int _{-\infty }^{\infty }g(c+ix)e^{-ux}e^{icu}\,dx.

這裡就可以套用此拉普拉斯方法求漸進解，最後，再利用 u = t / i 把 t 換回來，就可以得到該拉普拉斯逆變換的漸進解了。

例子1：斯特靈公式

拉普拉斯方法可以用在推導斯特靈公式上；當 N 很大時，

N!\approx {\sqrt {2\pi N}}N^{N}e^{-N}\,

證明：

由 Γ函数的積分定義，我們可以得到

N!=\Gamma (N+1)=\int _{0}^{\infty }e^{-x}x^{N}\,dx.

接著讓我們做變數變換，

x=Nz\,

因此

dx=N\,dz.

將這些代回 Γ函数的積分定義裡，我們可以得到

{\begin{aligned}N!&=\int _{0}^{\infty }e^{-Nz}\left(Nz\right)^{N}N\,dz\\&=N^{N+1}\int _{0}^{\infty }e^{-Nz}z^{N}\,dz\\&=N^{N+1}\int _{0}^{\infty }e^{-Nz}e^{N\ln z}\,dz\\&=N^{N+1}\int _{0}^{\infty }e^{N(\ln z-z)}\,dz.\end{aligned}}

經由此變數變換後，我們有了拉普拉斯方法所需要的 $f(x)$ 為

f\left(z\right)=\ln {z}-z

而它乃為二次可微函數，且

f'(z)={\frac {1}{z}}-1,\,

f''(z)=-{\frac {1}{z^{2}}}.\,

因此， ƒ(z) 的極大值出現在 z₀ = 1 而且在該點的二次微分為 $-1$ 。因此，我們得到

N!\approx N^{N+1}{\sqrt {\frac {2\pi }{N}}}e^{-N}={\sqrt {2\pi N}}N^{N}e^{-N}.\,

例子2：貝氏網路，參數估計與概率推理

關於概率推理的簡介，請參考 http://doc.baidu.com/view/e9c1c086b9d528ea81c77989.html 。而在 Azevedo-Filho & Shachter 1994 的文章裡，則回顧了如何應用此拉普拉斯方法 (無論是單變數或者多變數) 如何應用在 概率推理 上，以加速得到系統的後驗矩 (數學) (posterior moment) ，貝氏參數等，並舉醫學診斷上的應用為例。

參考文獻

Butler, Ronald W. . Cambridge University Press. 2007. ISBN 978-0-521-87250-8.
MacKay, David J. C. . Cambridge: Cambridge University Press. September 2003. ISBN 9780521642989. （原始内容存档于2016-02-17）.

Deift, P.; Zhou, X., , Ann. of Math. 137 (2), 1993, 137 (2): 295–368, doi:10.2307/2946540.
Azevedo-Filho, A.; Shachter, R., , Mantaras, R.; Poole, D. (编), , San Francisco, CA: Morgan Kauffman, 1994, CiteSeerX: 10.1.1.91.2064.
Erdelyi, A., , Dover Publications, 2012, ISBN 9780486155050.
Arfken, G.B.; Weber, H.J., , Elsevier Science, 2005, ISBN 9780080470696.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Butler, Ronald W. . Cambridge University Press. 2007. ISBN 978-0-521-87250-8.

[2] MacKay, David J. C. . Cambridge: Cambridge University Press. September 2003. ISBN 9780521642989. （原始内容存档于2016-02-17）.