指数分布
在機率論和統計學中,指數分布(英語:)是一種連續機率分佈。指數分布可以用来建模平均发生率恒定、连续、独立的事件發生的間隔,比如旅客進入機場的時間間隔、電話打進客服中心的時間間隔、中文維基百科新條目出現的時間間隔、機器的壽命等。
|
密度函數 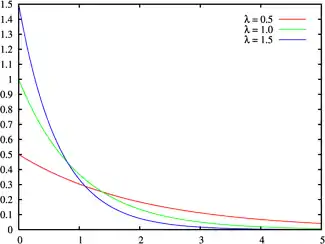 | |||
|
累積分布函數 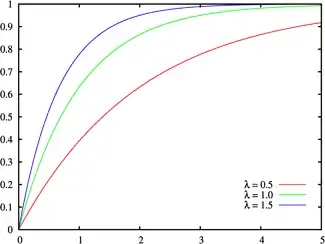 | |||
| 率 | |||
| 值域 | |||
| 累積分布函數 | |||
| 期望值 | |||
| 中位數 | |||
| 眾數 | |||
| 偏度 | |||
| 峰度 | |||
| 熵 | |||
| 特徵函数 | |||
記號
若隨機變數服从母數為或的指数分布,則記作
或
兩者意義相同,只是與互為倒數關係。只要將以下式子做的替換即可,即,指數分布之機率密度函數為:
或
累积分布函数為:
或
其中λ > 0是分布的母數,即每单位时间发生该事件的次数; β 為比例母數,即該事件在每單位時間內的發生率。兩者常被称为率参数(rate parameter)。指数分布的区间是[0,∞)。
特性
与泊松过程的关系
泊松過程是一种重要的随机过程。泊松過程中,第k次随机事件与第k+1次随机事件出现的时间间隔服从指数分布。而根据泊松過程的定义,长度为t的时间段内没有随机事件出现的概率等于
- ,
长度为t的时间段内随机事件发生一次的概率等于 , 所以第k次随机事件之后长度为t的时间段内,第k+n次 (n=1, 2, 3,...)随机事件出现的概率等于。这是指数分布。这还表明了泊松过程的无记忆性。
参数估计
参考文獻
- Donald E. Knuth (1998). The Art of Computer Programming, volume 2: Seminumerical Algorithms, 3rd edn. Boston: Addison-Wesley. ISBN 0-201-89684-2. pp. 133
- Luc Devroye (1986). Non-Uniform Random Variate Generation. New York: Springer-Verlag. ISBN 0-387-96305-7. pp. 392–401
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.