斯梅爾悖論
差拓扑结构中,球面外翻(Sphere eversion)是指在三维空间中,將球面從內向外翻。值得注意的是,我們有辦法在不割開、撕裂或製造摺痕的前提下,連續且光滑地將球面由內向外翻(有可能產生自交)。 這對非数学家甚至是瞭解定期同伦的人來說都十分意外,并可以被视为一种真詭論:乍看下是假,實際上為真。
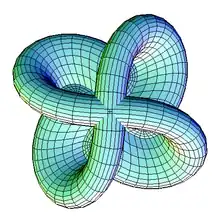
一 Morin曲面的俯視圖
更準確地说,令
使得ƒ0 = ƒ 且 ƒ1 = −ƒ。
歷史
無摺痕球面外翻的存在性證明是由史蒂芬·斯梅爾於1957年率先完成。雖然已經有一些電腦動畫幫助人們想像,但很難提供這種翻轉的動畫片。第一个展示性的例子經過數位数学家的努力才完成,包括弗拉基米爾·阿諾爾德和盲人數學家伯纳德·莫兰。另一方面,证明这样的「翻轉」存在容易多了,这就是斯梅尔證明的事。
剛開始斯梅尔的博士指導老師拉乌尔·博特告诉他這件事显然是错误的(Levy 1995)。他的推論是,映射度的高斯映射必须保存在这种「翻轉」—特别地,這表示在R2沒有这种S1的翻轉。但在R3中, 嵌入f 和 −f對應的高斯映射 在 R3 都等于1,并且没有相反的符号作猜测。 所有 R3 中S2的浸入,它對應的高斯映射映射度都是1,所以没有問題。「真悖论」也许更适合用在这个级别:在斯梅尔的工作之前,没有任何嘗試論證或反正外翻 S2的紀錄,所以歷史上並沒有關於球面外翻的紀錄,只有第一次面對視覺化球面外翻的人,所留下對其精妙之處的讚揚。
進一步的一般化在h-原理。
參考文獻
- Levy, Silvio, , , Wellesley, MA: A K Peters Ltd., 1995 [2017-06-03], ISBN 978-1-56881-049-2, MR 1357900, (原始内容存档于2017-09-09)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.