斯特灵数
在數學中,史特靈數用於解決各種數學分析和組合數學問題,史特靈數是兩組不同的數,均是18世紀由詹姆士·史特靈引入並以其命名,以第一類史特靈數和第二類史特靈數的稱呼區分。此外,有時候也將拉赫數稱爲第三類史特靈數[1]。
第一類史特靈數
定義
第一類史特靈數可以定義爲對應遞降階乘展開式的各項係數,即
其中,()即爲第一類史特靈數。例如:
則
於是, , , 。
由此可知,是代數數,或稱爲有符號(第一類)史特靈數(英語:signed Stirling numbers of the first kind)。
有符號史特靈數的絕對值可以看作(或直接定義爲)把個元素排列成個非空圓圈(循環排列)的方法數目。所以是算術數,或稱爲無符號(第一類)史特靈數(英語:unsigned Stirling numbers of the first kind)。無符號史特靈數一般可以記爲或。例如:把,,三個數排列成個非空圓圈,顯然有零種方法;排列成個非空圓圈,有,兩種方法;排列成個非空圓圈,有,和三種方法;排列成個非空圓圈,有一種方法,所以,,。可以看到這和前面有符號史特靈數在時的結果一致(只是符號差異)。
與有符號史特靈數類似,無符號史特靈數可以定義爲對應遞進階乘展開式的各項係數,即
其中,()即爲無符號史特靈數。不過要注意,這裏的記號有時候會用來表示高斯二项式系数。
有符號史特靈數和無符號史特靈數有如下關係:
拓展示例
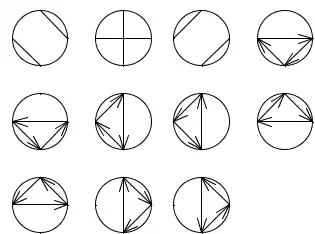
無符號史特靈數有更多的應用。例如,將個元素分成組,每組內的元素再進行排列的方法數目即可用無符號史特靈數求得。以爲例:
- (A,B)(C,D)
- (A,C)(B,D)
- (A,D)(B,C)
- (A)(B,C,D)
- (A)(B,D,C)
- (B)(A,C,D)
- (B)(A,D,C)
- (C)(A,B,D)
- (C)(A,D,B)
- (D)(A,B,C)
- (D)(A,C,B)
或用有向圖表示如下:
遞推關係式
無符號史特靈數有如下遞推關係式:
其中,,且初始條件爲 ,()。
有符號史特靈數有如下遞推關係式:
第一類史特靈數表
下表其實是一部分無符號史特靈數,要想獲得有符號史特靈數,可以通過它們之間的關係式:
求得。
k n |
0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||
| 1 | 0 | 1 | |||||
| 2 | 0 | 1 | 1 | ||||
| 3 | 0 | 2 | 3 | 1 | |||
| 4 | 0 | 6 | 11 | 6 | 1 | ||
| 5 | 0 | 24 | 50 | 35 | 10 | 1 | |
| 6 | 0 | 120 | 274 | 225 | 85 | 15 | 1 |
第二類史特靈數
定義
第二類史特靈數與第一類史特靈數類似,可以用遞降階乘定義爲
其中,[2][3]即爲第二類史特靈數,也可以記爲[4]。例如:
即
將遞降階乘展開並合併同類項,得
比較等式兩邊係數,得
解得
,,,。
第二類史特靈數計算的是將含有個元素的集合拆分爲個非空子集的方法數目[5]。例如:對於集合,若拆分爲個非空子集,顯然有零種方法;拆分爲個非空子集,只有一種方法;拆分爲個非空子集,有,,三種方法;拆分爲個非空子集,有一種方法。於是,,,。
第二類史特靈數可以使用以下公式進行計算:[6]
取進行驗算,有
即
於是
拓展示例
將個人分成組的分組方法的數目。例如有甲、乙、丙、丁四人,若所有人分成組,只能所有人在同一組,因此;若所有人分成組,只能每人獨立一組,因此;若分成組,可以是甲乙一組、丙丁一組,或甲丙一組、乙丁一組,或甲丁一組、乙丙一組,或其中三人同一組另一人獨立一組,即:
- {甲, 乙}{丙, 丁}
- {甲, 丙}{乙,丁}
- {甲, 丁}{乙, 丙}
- {甲}{乙, 丙, 丁}
- {乙}{甲, 丙, 丁}
- {丙}{甲, 乙, 丁}
- {丁}{甲, 乙, 丙}
因此。同理,可以得到。
遞推關係式
第二類史特靈數有與第一類史特靈數類似的遞推關係式:
其中,,且初始條件爲 ,()。
第二類史特靈數表
下面爲部分第二類史特靈數:
k n |
0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||
| 1 | 0 | 1 | |||||
| 2 | 0 | 1 | 1 | ||||
| 3 | 0 | 1 | 3 | 1 | |||
| 4 | 0 | 1 | 7 | 6 | 1 | ||
| 5 | 0 | 1 | 15 | 25 | 10 | 1 | |
| 6 | 0 | 1 | 31 | 90 | 65 | 15 | 1 |
簡單性質
觀察前面的“第二類史特靈數表”,我們可以得到一些簡單的性質:
- ,()。
如果,我們有
- ;
或更一般地,如果,我們有
- 。
還有
- ,
- ,
- ,
- ,
- ,
- ,
- 。
拉赫數
定義
拉赫數是由伊沃·拉赫在1954年發現的[7][8],因爲拉赫數與史特靈數關係密切,所以有時拉赫數也被稱爲第三類史特靈數。可以用遞進階乘和遞降階乘定義爲
或
其中, 即爲拉赫數。例如:
即
等式兩邊展開並合併同類項,得
比較等式兩邊係數,得
解得 ,, ,。
或
即
等式兩邊展開並合併同類項,得
比較等式兩邊係數,得
解得 ,, ,。
以上定義的拉赫數是無符號拉赫數(英語: signed Lah numbers),有符號拉赫數(英語:signed Lah numbers)的定義如下:
或
無符號拉赫數計算的是將含有個元素的集合拆分爲個非空線性有序子集的方法數目[9]。例如:對於集合,若拆分爲個非空線性有序子集,顯然有零種方法;拆分爲個非空線性有序子集,有,,,,,六種方法;拆分爲個非空線性有序子集,有,,,,,六種方法;拆分爲個非空線性有序子集,有,,一種方法。於是,, ,。
無符號拉赫數可以使用以下公式進行計算:
有符號拉赫數可以使用以下公式進行計算:
拓展示例

遞推關係式
無符號拉赫數有如下遞推關係:
或
其中,,,(),
拉赫數表
下面爲部分無符號拉赫數:
k n |
0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||
| 1 | 0 | 1 | |||||
| 2 | 0 | 2 | 1 | ||||
| 3 | 0 | 6 | 6 | 1 | |||
| 4 | 0 | 24 | 36 | 12 | 1 | ||
| 5 | 0 | 120 | 240 | 120 | 20 | 1 | |
| 6 | 0 | 720 | 1800 | 1200 | 300 | 30 | 1 |
簡單性質
觀察前面的“拉赫數表”,我們可以得到一些簡單性質:
, ()
如果,有 ,
還有
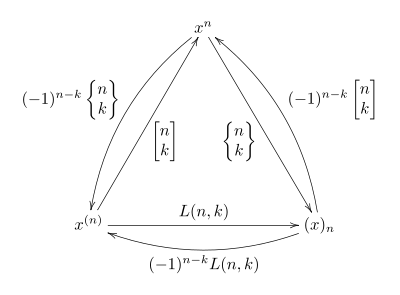
三類之間的關係
三類史特靈數以及乘方、階乘之間的關係可以用下圖表示:
參考資料
- Sándor, Jozsef; Crstici, Borislav. . Kluwer Academic Publishers. 2004: 464. ISBN 9781402025464.
- . Imanuel Marx, The American Mathematical Monthly 69, #6 (June–July 1962). : 530–532,. JSTOR 2311194..
- Antonio Salmeri (编). . : pp. 44–54.
- Knuth, D.E. (1992) (编). . : 403-422. JSTOR 2325085. arXiv:math/9205211
 . doi:10.2307/2325085.
. doi:10.2307/2325085. - Brualdi,R.A. (编). . 由冯速等人翻译. 北京: 机械工业出版社. 2012.4: 176页. ISBN 978-7-111-37787-0.
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2019-06-06]. (原始内容存档于2019-06-06) (英语).
- Lah, Ivo. 9. 1954: 7–15.
|journal=被忽略 (帮助) - John Riordan, Introduction to Combinatorial Analysis (页面存档备份,存于), Princeton University Press (1958, reissue 1980) ISBN 978-0-691-02365-6 (reprinted again in 2002 by Dover Publications).
- Petkovsek, Marko; Pisanski, Tomaz. 12. Fall 2007: 417–424. JSTOR 24340704.
|journal=被忽略 (帮助);|number=被忽略 (帮助) - Comtet, Louis. . Dordrecht, Holland: Reidel. 1974: 156.