极值点
数学中,极值点(arguments of the maxima/minima,分别缩写为arg max/arg min或argmax/argmin)是使函数输出值取得极值的输入点。[note 1]函数的自变量在定义域上,因变量则在到达域上。
定义
若或S在语境中明确,则通常省略S,如也就是说,是点x的集合,使到达函数最大值(若存在)。可以是空集、单元集,或包含多个元素。
在凸分析与变分分析中,(是广义实数)的情形时的定义略有不同。[2]这时,若f等同于S上的,则(即),否则定义如上,这时也可以写成
这里要强调的是,这个涉及的等式只有当f在S上不等同于时才成立。[2]
例子与性质
例如,若,则f只有在这一点上取最大值1。因此
算子与不同,给定相同的函数时,后者返回函数极大值,而不是使函数取得极大值的点。也就是说
- is the element in
max可以是空集(这时极大值未定义),这与相同;不同的是可能不含多个元素。[note 2]例如,取则但因为函数在的每个元素上都取相同的值。
等价地,若M是f的极大值,则是极大值的水平集:
可以将其重排,得到简单的等式[note 3]
若极大值点只有一个,那么应被视为一个点,而非点集。例如
(而非单元集),因为的极大值25仅在时取到。[note 4]而若在多个点上都取得极大值,就应被视为点集。例如
因为maximum value of 的极大值1在时取到。在整条实数线上
- 因此是无限集。
函数不必达到极大值,因此有时是空集。例如,因为在实数线上无界。再举个例子,,虽然有界(),但由极值定理,闭区间上的连续实值函数必有极大值,因此有非空的。
注释
参考文献
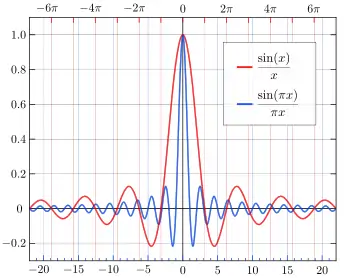
- "The Unnormalized Sinc Function 的存檔,存档日期2017-02-15.", University of Sydney
- Rockafellar & Wets 2009,第1-37頁.
- Rockafellar, R. Tyrrell; Wets, Roger J.-B. . Grundlehren der mathematischen Wissenschaften 317. Berlin New York: Springer Science & Business Media. 26 June 2009. ISBN 9783642024313. OCLC 883392544.
外部链接
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.