标量乘法

标量乘法（英語：）是線性代數中向量空間的一種基本運算[1][2][3]（更廣義的，是抽象代數的一個模）[4][5])。在直覺上，將一個實數向量和一個正的實數進行标量乘法，也就是將其長度乘以此标量，方向不變。标量一詞也從此用法而來：可將向量缩放的量。标量乘法是將標量和向量相乘，結果得到一向量，和內積將兩向量相乘，得到一純量不同。

  提示：此条目页的主题不是點積。
「标量乘法」的各地常用名稱
中国大陸
臺灣
用标量乘法得到一向量的三倍
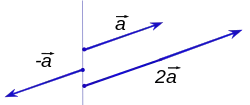
向量a的标量乘法，−a和2a

定義

若K為域，而V為K上的向量空間，标量乘法為從K× V到V的函数。將K中的c和V中的v計算标量乘法，結果記為cv。

性質

标量乘法符合以下的規則：（粗表示向量）

  • 标量的加成性：(c + d)v = cv + dv；
  • 向量的加成性：c(v + w) = cv + cw；
  • 标量相乘和标量乘法的結合律：(cd)v = c(dv)；
  • 乘以1不會改變向量：1v = v；
  • 乘以0會得到零向量：0v = 0；
  • 乘以-1會得到加法逆元：(−1)v = −v.

其中+表示域或是向量空間的加法，0是域或是向量空間的加法單位元

詮釋

标量乘法可以視為是向量空間的外部二元运算或域的群作用。标量乘法的幾何詮釋是向量的拉長，方向可能會對調。

标量乘法中，V也可以是K，則标量乘法就變成域中的乘法。

若V是Kn，标量乘法等於向量中的每一個元素都和標量相乘，需另外定義。

若K是交换环而V是K上的模，同樣的定義仍可以適用。 K甚至可以是一個半環，但沒有加法逆元。若K不符合交換律，可以定義左标量乘法cv和右標量乘法vc。

相關

參考資料
  1. Lay, David C. 3rd. Addison–Wesley. 2006. ISBN 0-321-28713-4.
  2. Strang, Gilbert. 4th. Brooks Cole. 2006. ISBN 0-03-010567-6.
  3. Axler, Sheldon. 2nd. Springer. 2002. ISBN 0-387-98258-2.
  4. Dummit, David S.; Foote, Richard M. 3rd. John Wiley & Sons. 2004. ISBN 0-471-43334-9.
  5. Lang, Serge. . Graduate Texts in Mathematics. Springer. 2002. ISBN 0-387-95385-X.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.