欧拉公式

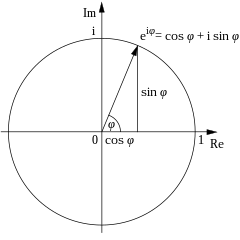
這公式可以說明當 ${\displaystyle x}$ 為實數時，函數 ${\displaystyle e^{ix}}$ 可在複數平面描述一單位圓。且 ${\displaystyle x}$ 為此平面上一條連至原點的線與正實數軸的交角。先前一個在複數平面的複點只能用笛卡尔坐标系描述，歐拉公式在此提供複點至極坐標的變換

任何複數 ${\displaystyle z=x+yi}$ 皆可記為

${\displaystyle z=x+iy=|z|(\cos \phi +i\sin \phi )=|z|e^{i\phi }\,}$

${\displaystyle {\bar {z}}=x-iy=|z|(\cos \phi -i\sin \phi )=|z|e^{-i\phi }\,}$

在此

${\displaystyle x=\mathrm {Re} \{z\}\,}$為實部

${\displaystyle y=\mathrm {Im} \{z\}\,}$為虛部

${\displaystyle |z|={\sqrt {x^{2}+y^{2}}}}$為 ${\displaystyle z}$ 的模

${\displaystyle \phi =\mathrm {atan2} {(y,x)}}$，其中 ${\displaystyle \mathrm {atan2} {(y,x)}={\begin{cases}\arctan \left({\frac {y}{x}}\right)&\qquad x>0\\\pi +\arctan \left({\frac {y}{x}}\right)&\qquad y\geq 0,x<0\\-\pi +\arctan \left({\frac {y}{x}}\right)&\qquad y<0,x<0\\{\frac {\pi }{2}}&\qquad y>0,x=0\\-{\frac {\pi }{2}}&\qquad y<0,x=0\\{\text{undefined}}&\qquad y=0,x=0\end{cases}}}$

約翰·伯努利注意到有[4]

${\displaystyle {\frac {1}{1+x^{2}}}={\frac {1}{2}}\left({\frac {1}{1-ix}}+{\frac {1}{1+ix}}\right).}$

并且由于

${\displaystyle \int {\frac {dx}{1+ax}}={\frac {1}{a}}\ln(1+ax)+C,}$

上述公式通过把自然对数和复数（虚数）联系起来，告诉我们关于複對數的一些信息。然而伯努利并没有计算出这个积分。

欧拉也知道上述方程，伯努利对欧拉的回应表明他还没有完全理解复对数。欧拉指出复对数可以有无穷多个值。

与此同时，罗杰·柯特斯于 1714 年发现[5]

${\displaystyle ix=\ln(\cos x+i\sin x).}$

由于三角函数的周期性，一个复数可以加上 2iπ 的不同倍数，而它的复对数可以保持不变。

1740年左右，欧拉把注意力从对数转向指数函数，得到了以他命名的欧拉公式。欧拉公式通过比较指数的级数展开和三角函数得到（其实此证法存在问题，原因见验证方法，但结论正确。），于1748年发表[6][5]。

大约50年之后，卡斯帕尔·韦塞尔提出可以把复数視做复平面中的点。

对于任意实数${\displaystyle x\,}$，以下等式恆成立：

${\displaystyle e^{ix}=\cos x+i\sin x}$

由此也可以推导出

${\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}}$及${\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}}$。

当${\displaystyle x=\pi \,}$时，欧拉公式的特殊形式为

${\displaystyle {{{e}^{{i}\,{\pi }}}+{1}}=0}$。

首先，在复数域上对${\displaystyle e^{x}\,}$进行定义：

对于${\displaystyle a,b\in \mathbb {R} ,c=a+ib\in \mathbb {C} }$，规定${\displaystyle e^{c}=\lim _{n\rightarrow \infty }(1+{\frac {c}{n}})^{n}}$。

对复数的极坐标表示${\displaystyle w=u+iv=r(\cos \theta +i\sin \theta )}$，有：

${\displaystyle r={\sqrt {u^{2}+v^{2}}}\in \mathbb {R} ,\theta =\arctan({\frac {v}{u}})\in \mathbb {R} }$

且根据棣莫弗公式，${\displaystyle w^{n}=(u+iv)^{n}=r^{n}(\cos n\theta +i\sin n\theta )}$

从而有：

${\displaystyle (1+{\frac {a+bi}{n}})^{n}=[(1+{\frac {a}{n}})+i{\frac {b}{n}}]^{n}=r_{n}(\cos \theta _{n}+i\sin \theta _{n})}$

假设${\displaystyle n>|a|}$，则：

${\displaystyle r_{n}=[(1+{\frac {a}{n}})^{2}+({\frac {b}{n}})^{2}]^{\frac {n}{2}},\theta _{n}=n\arctan {\frac {\frac {b}{n}}{1+{\frac {a}{n}}}}}$

（由於包含n在冪，所以要ln）从而有：

${\displaystyle {\begin{aligned}\lim _{n\rightarrow \infty }\ln r_{n}&=\lim _{n\rightarrow \infty }[{\frac {n}{2}}\ln(1+{\frac {2a}{n}}+{\frac {a^{2}+b^{2}}{n^{2}}})]\\&=\lim _{n\rightarrow \infty }[{\frac {n}{2}}({\frac {2a}{n}}+{\frac {a^{2}+b^{2}}{n^{2}}})]\\&=a\\\end{aligned}}}$

這一步驟用到 ${\displaystyle \ln(1+x)\approx x}$（墨卡托級數）

即：

${\displaystyle \lim _{n\rightarrow \infty }r_{n}=\lim _{n\rightarrow \infty }e^{\ln r_{n}}=e^{a}}$

又有(arctan x 約等於x 於0附近）：

${\displaystyle {\begin{aligned}\lim _{n\rightarrow \infty }\theta _{n}&=\lim _{n\rightarrow \infty }(n\arctan {\frac {\frac {b}{n}}{1+{\frac {a}{n}}}})\\&=\lim _{n\rightarrow \infty }(n{\frac {\frac {b}{n}}{1+{\frac {a}{n}}}})\\&=b\\\end{aligned}}}$

从而可以证明：

${\displaystyle \lim _{n\rightarrow \infty }(1+{\frac {a+bi}{n}})^{n}=e^{a}(\cos b+i\sin b)}$

即：

${\displaystyle e^{a+ib}=e^{a}(\cos b+i\sin b)}$

令${\displaystyle a=0}$，可得欧拉公式。

证毕。[7]

方法一：泰勒级数

把函数${\displaystyle e^{x}\,}$、${\displaystyle \cos x\,}$和${\displaystyle \sin x\,}$写成泰勒级数形式：

${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots }$

${\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots }$

${\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots }$

将${\displaystyle x=iz\,}$代入${\displaystyle e^{x}\,}$可得：

${\displaystyle {\begin{aligned}e^{iz}&=1+iz+{\frac {(iz)^{2}}{2!}}+{\frac {(iz)^{3}}{3!}}+{\frac {(iz)^{4}}{4!}}+{\frac {(iz)^{5}}{5!}}+{\frac {(iz)^{6}}{6!}}+{\frac {(iz)^{7}}{7!}}+{\frac {(iz)^{8}}{8!}}+\cdots \\&=1+iz-{\frac {z^{2}}{2!}}-{\frac {iz^{3}}{3!}}+{\frac {z^{4}}{4!}}+{\frac {iz^{5}}{5!}}-{\frac {z^{6}}{6!}}-{\frac {iz^{7}}{7!}}+{\frac {z^{8}}{8!}}+\cdots \\&=\left(1-{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}-{\frac {z^{6}}{6!}}+{\frac {z^{8}}{8!}}-\cdots \right)+i\left(z-{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}-{\frac {z^{7}}{7!}}+\cdots \right)\\&=\cos z+i\sin z\end{aligned}}}$

方法二：求導法

对于所有${\displaystyle x\in I}$，定義函數${\displaystyle f(x)={\frac {\cos x+i\sin x}{e^{ix}}}}$

由於${\displaystyle e^{ix}\cdot e^{-ix}=e^{0}=1}$

可知${\displaystyle e^{ix}\,}$不可能為0，因此以上定義成立。

${\displaystyle f(x)\,}$之导数為：

${\displaystyle {\begin{aligned}f'(x)&={\frac {(-\sin x+i\cos x)\cdot e^{ix}-(\cos x+i\sin x)\cdot i\cdot e^{ix}}{(e^{ix})^{2}}}\\&={\frac {-\sin x\cdot e^{ix}-i^{2}\sin x\cdot e^{ix}}{(e^{ix})^{2}}}\\&={\frac {-\sin x\cdot e^{ix}+\sin x\cdot e^{ix}}{(e^{ix})^{2}}}\\&=0\end{aligned}}}$

设${\displaystyle [a,b]\in I}$和${\displaystyle c\in (a,b)}$

${\displaystyle f'(c)={\frac {f(b)-f(a)}{b-a}}.}$（拉格朗日中值定理）

${\displaystyle \because f'(x)=0}$

${\displaystyle \therefore f'(c)=0}$

${\displaystyle f(a)=f(b)}$

因此${\displaystyle f(x)\,}$必是常數函數。

${\displaystyle f(x)=f(0)}$

${\displaystyle }$

${\displaystyle {\frac {\cos x+i\sin x}{e^{ix}}}={\frac {\cos 0+i\sin 0}{e^{0}}}=1}$

重新整理，即可得到：

${\displaystyle e^{ix}=\cos x+i\sin x}$

方法三：微積分

找出一个原函數${\displaystyle y(x)}$，使得${\displaystyle {\frac {dy}{dx}}=iy}$及${\displaystyle y(0)=1}$。

假设 ${\displaystyle y(x)=e^{ix}}$，有：

${\displaystyle {\frac {d}{dx}}e^{ix}=ie^{ix}=iy}$

假设 ${\displaystyle y(x)=i\sin x+\cos x}$，有：

${\displaystyle {\begin{aligned}{\frac {d}{dx}}(\cos x+i\sin x)&=-\sin x+i\cos x\\&=i(i\sin x+\cos x)\\&=iy\end{aligned}}}$

使用積分法，可得${\displaystyle iy}$的原函數是以上兩個函數分别与任意实数的和，分别记为：

${\displaystyle y_{1}(x)=e^{ix}+C_{1}}$

${\displaystyle y_{2}(x)=\cos x+i\sin x+C_{2}}$

其中，${\displaystyle \mathbb {C} _{1}}$和:${\displaystyle \mathbb {C} _{2}}$是任意实数。

又${\displaystyle x=0}$時，${\displaystyle y(0)=1}$，观察到：

${\displaystyle y_{1}(0)=e^{i0}+C_{1}=e^{0}+C_{1}=1+C_{1}}$

${\displaystyle y_{2}(0)=\cos 0+i\sin 0+C_{2}=1+i(0)+C_{2}=1+C_{2}}$

所以${\displaystyle C_{1}=C_{2}=0}$，可以得出：

${\displaystyle {\begin{aligned}y(x)&=e^{ix}=\cos x+i\sin x\end{aligned}}}$

在複分析領域，歐拉公式亦可以以函數的形式表示

${\displaystyle \operatorname {cis} \theta =\cos \theta +i\sin \theta }$

${\displaystyle \operatorname {cis} \theta =e^{i\theta }}$

並且一般定義域為${\displaystyle \theta \in \mathbb {R} \,}$，值域為${\displaystyle \theta \in \mathbb {C} \,}$（复平面上的所有单位向量）。

當一複數的模為1，其反函數就是輻角（arg函數）。

當${\displaystyle \theta }$值為複數時，cis函數仍然是有效的，所以有些人可利用cis函數將歐拉公式推廣到更複雜的版本。[2]

由於${\displaystyle e^{i\alpha }=\cos \alpha +i\sin \alpha }$且${\displaystyle e^{i\beta }=\cos \beta +i\sin \beta }$，則有

${\displaystyle {\begin{aligned}e^{i(\alpha +\beta )}&=\cos(\alpha +\beta )+i\sin(\alpha +\beta )=e^{i\alpha +i\beta }\\&=e^{i\alpha }\times e^{i\beta }\\&=(\cos \alpha +i\sin \alpha )\times (\cos \beta +i\sin \beta )\\&=(\cos \alpha \times \cos \beta +i\sin \alpha \times i\sin \beta )+(i\sin \alpha \times \cos \beta +\cos \alpha \times i\sin \beta )\\&=(\cos \alpha \cos \beta -\sin \alpha \sin \beta )+i(\sin \alpha \cos \beta +\cos \alpha \sin \beta )\\\end{aligned}}}$

實部等於實部，虛部等於虛部，因此

${\displaystyle \cos(\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta }$

${\displaystyle \sin(\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta }$

• cis函數
• 歐拉恆等式