機率密度函數

对于一维实随机变量X，设它的累积分布函数是${\displaystyle F_{X}(x)}$。如果存在可测函数 ${\displaystyle f_{X}(x)}$，满足：

${\displaystyle \forall -\infty <a<\infty ,\quad F_{X}(a)=\int _{-\infty }^{a}f_{X}(x)\,dx}$

那么X 是一个连续型随机变量，并且${\displaystyle f_{X}(x)}$是它的概率密度函数。[2]

连续型均匀分布的概率密度函数

最简单的概率密度函数是均匀分布的密度函数。对于一个取值在区间${\displaystyle [a,b]}$上的均匀分布函数${\displaystyle \mathbf {I} _{[a,b]}}$，它的概率密度函数：

${\displaystyle f_{\mathbf {I} _{[a,b]}}(x)={\frac {1}{b-a}}\mathbf {I} _{[a,b]}}$

也就是说，当x 不在区间${\displaystyle [a,b]}$上的时候，函数值等于0，而在区间${\displaystyle [a,b]}$上的时候，函数值等于${\displaystyle \scriptstyle {\frac {1}{b-a}}}$ 。这个函数并不是完全的连续函数，但是是可积函数。

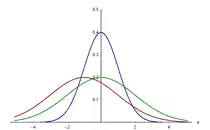
正态分布的概率密度函数

正态分布是重要的概率分布。它的概率密度函数是：

${\displaystyle f(x)={1 \over \sigma {\sqrt {2\pi }}}\,e^{-{(x-\mu )^{2} \over 2\sigma ^{2}}}}$

随着参数${\displaystyle \mu }$和${\displaystyle \sigma }$变化，概率分布也产生变化。

随机变量X的n阶矩是X的n次方的期望值，即

${\displaystyle \mathbb {E} [X^{n}]=\int _{-\infty }^{\infty }x^{n}f_{X}(x)\,dx}$

X的方差为

${\displaystyle \sigma _{X}^{2}=\mathbb {E} \left[\left(X-\mathbb {E} [X]\right)^{2}\right]=\int _{-\infty }^{\infty }(x-E[X])^{2}f_{X}(x)\,dx}$

更广泛的说，设${\displaystyle g}$ 为一个有界连续函数，那么随机变量${\displaystyle g(X)}$的数学期望

${\displaystyle \mathbb {E} [g(X)]=\int _{-\infty }^{\infty }g(x)f_{X}(x)\,dx}$[3]

對機率密度函數作类似傅立葉變換可得特徵函數。

${\displaystyle \Phi _{X}(j\omega )=\int _{-\infty }^{\infty }f(x)e^{j\omega x}\,dx}$

特徵函數與機率密度函數有一對一的關係。因此，知道一個分佈的特徵函數就等同於知道一個分佈的機率密度函數。[4]

• 概率分布
• 概率质量函数
• 累积分布函数
• 条件概率密度函数
• 核密度估计
• 似然函数