電荷
在電磁學裡,電荷(英語:)是构成物质的基本粒子的一種物理性質,原子中的质子和电子分别带有正电荷和负电荷,而中子不带电荷。[1]帶有電荷的物質稱為帶電物質,带有电荷的粒子称为带电粒子。两个帶電粒子之間會互相施加作用力,电荷符号相同的粒子会相互排斥,电荷符号不同的粒子会相互吸引,该作用力可由庫侖定律得出。
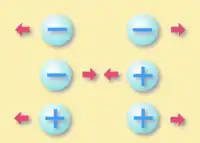
电荷是许多次原子粒子所拥有的一种基本守恒性质。电荷决定了带电粒子在电磁方面的物理行为。静止的带电粒子会产生电场,移动中的带电粒子会产生电磁场,带电粒子也会被电磁场所影响。一个带电粒子与电磁场之间的相互作用称为电磁力或电磁交互作用。这是四种基本交互作用中的一种。
物体所带过剩电荷的总量称为电荷量,简称电荷或电量。[1]电荷量的国际单位是庫侖(C),通常用符号Q表示。一个质子携带的电荷量称为基本电荷,约为1.602× 10-19库仑,用符号 表示,一个电子携带的电荷量为 。夸克携带的电荷量为e/3的倍数。
研究带电粒子相互作用的经典学术领域称为经典电动力学。假若量子效应可以被忽略,则经典电动力学能够很正确地描述出带电物质在电磁方面的物理行为。研究带电粒子与它们之间由光子媒介的相互作用的学术领域称为量子电动力学。
历史
西元前600年左右,希腊的哲学家泰勒斯记录,琥珀摩擦猫毛以后会吸引像羽毛一类的轻微物体,假若摩擦时间够久,甚至会有火花出现[2]。
1600年,英国医生威廉·吉尔伯特,对于电磁现象做了一个很仔细的研究。他指出琥珀並非唯一经过摩擦時會产生静电的物质,并且区分出电与磁不同的属性[3]。他撰写了第一本阐述电和磁的科学著作《论磁石》。吉尔伯特创建了新拉丁语的术语「electrica」(源自於「ήλεκτρον」,「ēlektron」,希腊文的「琥珀」),英文翻譯為「electrics」,意指如同琥珀一般當摩擦後會吸引微小物體的物質[4]。這新拉丁術語後來给出了英文術語「electricity」,最先出现于1646年,汤玛斯·布朗()的著作《Pseudodoxia Epidemica》(英文书名《Enquries into very many received tenets and commonly presumed truths》)[5]。随后,于1660年,科学家奥托·冯·格里克发明了可能是史上第一部静电发电机()。他将一个硫磺球固定于一根铁轴的一端,然后一边旋转硫磺球,一边用干手摩擦硫磺球,使硫磺球产生电荷,能够吸引微小物质[6]。
史蒂芬·戈瑞于1729年发现了电传导,即电荷可以从一个物质传导至另外一个物质的性質。只有某些種類的物质会传导电荷,其中,金属的能力最为优良。从此,科学家不再认为产生电荷的物体与所产生的电荷是不可分离的,而认为电荷是一种独立存在的物质,在那时被称为「电流体」。[7]1733年,查爾斯·篤費做實驗發現,假若被絲綢摩擦後的玻璃對於帶電的金葉片呈現出排斥的現象,則被羊毛摩擦後的琥珀會對這帶電的金葉片呈現出吸引的現象,因此,他将电分为两种,被絲綢摩擦後的玻璃帶有「玻璃電」,而被羊毛摩擦後的琥珀則帶有「樹脂電」。[4]:484-5这两种电会彼此相互抵销。这理论称为「雙流體理論」,是對於電現象首次給出解釋的電學理論。[8]:20稍後,美國科學家埃柏奈澤·肯納斯理也獨立獲得相同的結論。[9]:118
在十八世纪,美國人班杰明·富兰克林是电学最前端的专家之一,他认为「单流体理论」比较正确。他想像电储存于所有物质裡,并且通常处于平衡状态,而摩擦动作会使得电从一个物体流动至另一个物体。例如,他认为累积的电是储存于莱顿瓶的玻璃,用丝巾摩擦玻璃使得电从丝巾流动至玻璃。这流动形成了电流。他建议电量低于平衡的物体载有负电量,电量高于平衡的物体载有正电量。他任意地设定玻璃电为正电,具有多余的电;而琥珀电为负电,缺乏足够的电。同时期,英國學者威廉·沃森也獨立达到同样的结论。1747年,富兰克林假定在一个孤立系统内,总电荷量恒定,这称为电荷守恒定律。[7]:43-47[10]:1112
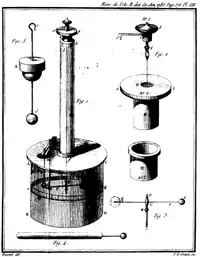
1785年,使用查尔斯·库仑与約翰·米歇爾分别独立发明的扭秤,库仑证实了约瑟夫·普利斯特里的基本定律:帶有静态电荷的两个物体彼此之间所感受的作用力与距离成平方反比。这奠定了静电的基本定律。[7]:56
剑桥大学卡文迪许实验室的约瑟夫·汤姆孙於1897年实验计算出組成阴极射线的粒子的電荷質量比。由於這數值與陰極物質、放電管內氣體無關,汤姆孙推斷,陰極射線的粒子源自於在陰極附近被強電場分解的氣體原子,這粒子為所有物質的組分。由於汤姆孙獲得的電荷質量比是電解實驗獲得的氫離子電荷質量比的千分之一倍,汤姆孙錯誤推斷,這粒子的質量很小,電荷很大,稍後他又修正為,粒子的帶電量等於電解單位電荷,而質量則為氫原子的千分之一。汤姆孙稱這粒子為「微粒」(corpuscle),就是微小粒子的意思,但學術界後來採用術語「電子」來標記這粒子。[11]1899年,汤姆孙實驗團隊做光電效應實驗與熱離子發射實驗測得於先前陰極射線等同的電荷質量比,這意味著這些實驗所涉及的粒子都是電子。[12]:23。由於汤姆孙建議電子為組成物質的基礎粒子,並且做實驗確切證實他的論述,他被公認為電子的發現者。電子是人類發現的第一種基礎粒子。[13]:40-43
1898年,汤姆孙做實驗發現,假設照射X射線於氣體,使用所產生的負離子來將過飽和水蒸氣凝結,則可以粗略測量帶電水滴的帶電量,其與電解實驗獲得的氫離子帶電量大約相等。隔年,他利用光電效應來進行類似實驗,仍舊獲得同樣結果。但是這些實驗所獲得的數值是很多帶電水滴的統計平均值,它們並未能證實所有電子的帶電量相等。美國物理學家羅伯特·密立根在1909年起完成一系列實驗測量電子的帶電量。起初,他使用水滴為測量對象,後來,由於油滴的蒸發率較低,他改使用油滴,[12]:23, 61在這些油滴實驗裏,他仔細地測量,帶電油滴在重力與電場的庫倫力的雙重影響下的懸浮運動。從獲得的數據,所有油滴的帶電量皆為同一數字的整倍數,因此認定此數值為單一電子的電荷,即基本電荷,並且斷定,電的基本結構是自然不可分的基本電荷,而不是多個不同數值的統計平均值。[14]:196-197俄國物理學者亞伯蘭·約費於1911年利用光電效應,照射紫外線於鋅金屬微粒子來製成帶電金屬微粒子,然後測量其帶電量,他也獨立獲得同樣結果。[15]
静电
假设在平衡状况,某物体的总电量不等于零,也就是说,这物体带有正电荷或负电荷,则称此物体带有静电。这方面的问题属于静电学领域。琥珀在经过用猫毛摩擦后,能够吸引轻小物体,这现象称为静电现象。这是负电荷从猫毛转移到琥珀后,所呈现的电性。当两个处于电势不相等的物体相互接触在一起,就会发生另外一种静电现象,称为静电放电,使得一个物体的电荷流动至另一个物体,从而促成电势相等。雷电是一种比较剧烈的静电放电现象。在大自然中,因为云层累积的正负电荷剧烈中和,会产生雷电和其所伴随的电光、雷声、热量。
点电荷

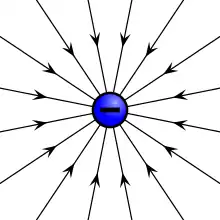
带电粒子时常被称为电荷,但电荷本身并非粒子,只是为了方便描述,可以将它想像成粒子。带电量多者称为具有较多电荷。处于一外电场的带电粒子,其所感受到的外电场的库仑力相依于其带电量。
点电荷是带电粒子的理想模型。真正的点电荷并不存在,只有当带电粒子之间的距离超大于粒子的尺寸,或是带电粒子的形状与大小对于彼此相互施加的作用力的影响能够被忽略时,可称此带电体为「点电荷」。
一个实际带电体能否视为点电荷,不仅与带电体本身有关,还取决于问题的性质和精确度的要求。点电荷是建立基本规律时必要的抽象概念,也是分析复杂问题时不可少的分析手段。例如,库仑定律、劳仑兹力定律的建立,带电体所产生的电场以及几个带电体之间彼此相互作用的定量研究,试验电荷的引入等等,都应用了点电荷的观念。
库仑定律
给予两个电量分别为、,位置分别为、的点电荷。根据库仑定律,点电荷作用于点电荷的力量的大小与方向,以方程式表达为
- 。
假若两个点电荷同性(电荷的正负号相同),则其电量的乘积是正值,两个点电荷互相排斥。反之,假若两个点电荷异性(电荷的正负号相反),则其电量的乘积是负值,两个点电荷互相吸引。
束缚电荷与自由电荷
有时候,虽然物体的总电量等于零,电荷分布可能会不均匀(例如,因为存在着外电场)。对于这状况,这物质称为电极化物质。束缚电荷是由于电极化而出现的电荷,束缚于原子内部。与束缚电荷明显不同,自由电荷是从外部置入的额外的电荷,不被束缚于原子内部。带电粒子朝着某方向的运动形成了电流,特别是在金属内部运动的电子。
粒子的电荷
在粒子物理学中,许多粒子都带有电荷。电荷在粒子物理学中是一个相加性量子数,电荷守恒定律也适用于粒子,反应前粒子的电荷之和等于反应后粒子的电荷之和,这对于强相互作用、弱相互作用、电磁相互作用都是严格成立的。
反粒子带有的电荷与对应粒子带有的电荷,电量相同,电性相异。夸克带有非整数电荷,不是-e/3,就是2e/3;但是科学家从未观察到单独夸克的存在(这事实可以用渐近自由()的理论来解释)。
电荷宇称时间对称
电荷宇称时间对称()对于粒子和反粒子的相对特性设下了强烈的约束。因此,可以严格地测试这理论。例如,质子和反质子的电荷的总和必须正好等于零。这全等式的精确度已经作实验测试至108分之一。使用潘宁阱()来囚禁反质子,质子和反质子的电荷质量比相等性质的精确度也被测试至6×109分之一[16]。
电荷守恒
电荷守恒定律表明,在一个孤立系统裏,不论发生什么变化,总电荷必定保持不变。所有物理程序都必须遵守这定律。在量子力学里,从波函数的规范不变性可以推导出这定律。
流入某體積的淨電流為
- ;
其中,是電流,是電流密度,是包圍體積的閉曲面,是微小面向量元素,垂直於從體積內朝外指出。
應用散度定理,將這方程式寫為
- 。
總電荷量與體積內的電荷密度的關係為
- 。
電荷守恆要求,流入體積的淨電流,等於體積內總電荷量的變率:
- 。
所以,
- 。
對於任意體積,上述方程式都成立。所以,可以將被積式提取出來:[17]
- 。
注释
参考文献
- . phy.sdu.edu.cn. [26 August 2023]. (原始内容存档于2023-08-25).
- Stewart, Joseph, , World Scientific: pp. 50, 2001, ISBN 9-8102-4471-1
- Simpson, Brian, , Elsevier Health Sciences: pp. 5–6, 2003, ISBN 0-4445-1258-6
- Benjamin, Park, , New York: J. Wiley: 315, 1898, ISBN 978-1313106054
- Chalmers, Gordon, , Philosophy of Science, 1937, 4 (1): pp. 75–95, doi:10.1086/286445
- Williams, Henry, , Harper: 170, [1904], ISBN 978-1151497598
- Whittaker, ET, , Nelson, London: pp. 37–44, 56, 1951
- Keithley, J.F. . IEEE Press. 1999. ISBN 0-7803-1193-0.
- Florian Cajori. . Macmillan. 1917.
- Ford, Guy (编), , F. E. Compton, 1922
- . Marriam-Webster, Inc. [2019-05-23]. (原始内容存档于2019-05-06).
a minute particle
- Buchwald, J.Z.; Warwick, A. . MIT Press. 2001. ISBN 978-0-262-52424-7.
- Kragh, Helge. Reprint. Princeton University Press. 2002. ISBN 978-0691095523.
- Greenberger, D.; Hentschel, K.; Weinert, F. (编), 2009th Edition, Springer, 2009, ISBN 978-3540706229
- Mikerov, Alexander, , St. Petersburg, Russia: IEEE, 2016, doi:10.1109/EIConRusNW.2016.7448102
|book-title=被忽略 (帮助) - G. Gabrielse, , International Journal of Mass Spectrometry, 2006, 251 (2–3): 273–280, doi:10.1016/j.ijms.2006.02.013
- Griffiths, David J., , Prentice Hall: pp. xiv, 213, 1998, ISBN 0-13-805326-X
