比恩模型

比恩模型所刻画的超导体内部场强在x方向上的空间分布随外加磁场的变化。左图初始的外加磁场为零（H = 0）；当H大于零且小于临界磁场H*，超导体内部的磁场分布如红线所示——场强随着深度增加呈线性递减，而中心部分保持超抗磁性，即磁场为零。橙线和黄线分别代表 H = H*，H > H* 的情况。右图始于左图的最终状态（黄线），磁场强度从 H > H* 开始减小然后反向增大，在达到临界磁场H*之前，超导体内部保持原有的磁场分布；而外侧出现了与原临界电流J_c大小相同，方向相反的超导电流，致使磁场强度分布出现如绿线所示的情况。蓝线和紫线分别表示 H = -H*，H < -H* 的情况。

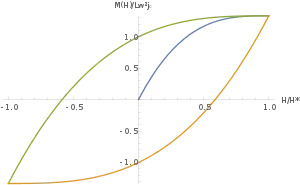
比恩模型考虑的是较强的磁通钉扎导致涡旋静止不动的情况。若施加一个均匀的外部磁场，比恩模型假设超导体内部的磁场强度会随着深度增加呈线性递减，斜率为4πJ_c/c（高斯单位制下）[3]，其中J_c为临界电流密度。此电流代表的是为了抵抗外界磁场而在超导体内部感应出的电流。临界电流的值在比恩模型中只能取三种值：+J_c、-J_c或0。临界磁场H*被定义为恰好完全消除超导体内部迈斯纳相（即磁场为零的区域）所需的外加磁场。当外加磁场 H < H*，超导体未被外部磁场穿透的部分保持迈斯纳相，中心部分的磁场强度为零（右图中的红线）。当 H = H*，外部磁场正好完全穿透超导体，内部磁场分布如右图的橙线所示。继续在同一方向增加磁场强度并不会改变场强和深度的线性关系，而只会将其整体平移（右图的黄线）；有人将其与沙堆（sandpile）进行类比[4][5]：对于一个沙堆，若沙堆的坡度达到了一个“临界值”，继续向上堆沙子不会增加沙堆的坡度（若坡度继续增加，则沙堆可能会因为不稳定而崩塌），而只增加整体的高度。基于这种“临界”的想法，比恩模型有时也会被称作“比恩临界态模型”（Bean's critical state model）。

若撤去外加磁场，超导体的内部将留下剩磁。在逐渐减小正向磁场至零后渐渐增大反向磁场的过程中，超导体内部可以被划分为两个区域（右图中的绿线）：靠近中心的区域的磁场梯度和撤去外场前保持一致，而靠近边缘的磁场梯度与其符号相反，大小一致。这是因为靠近中心的临界电流和靠近边缘的临界电流大小相等（均为J_c），方向相反。在反向磁场的强度增大到临界磁场H*以上（H = -H* 和 H < -H*）时，超导体内部再次只剩下一种临界态，磁场和临界电流的方向与之前 H = H* 时的方向正好相反（右图中的蓝线和紫线）。[6]

虽然比恩假设临界电流密度J_c为常数（即 H << H_c2 的条件下），但这只是一个比较粗略的估计。假设不同的临界电流密度可以在其他条件下得到更为精确的结果。例如，Kim 等人通过假设 1/J(H) 正比于 H 对比恩模型进行推广[7]，其理论计算结果与 Nb₃Sn 的测量结果相比极为吻合。另外，计算磁化强度时，样品不同的几何形状也是必须考虑的一点[8]。

• 理想硬超导体
• 超导现象
• 第二类超导体
• 迟滞现象