波形因數
應用
數位式的交流量測設備一般是針對弦波而設計的,例如許多交流電表會特別針對弦波的均方根值來進行調整。由於很難利用數位方式計算一訊號的均方根值,一般會改為計算弦波訊號的整流平均值,然後再乘以弦波的波形因數。不過若利用此方法計算其他波形的均方根值,會得到較不精確的結果[4]。
性質
波形因數是訊號的均方根值和整流平均值的比值,因此二個值之間類似及不同的性質決定了波形因數的性質。
例如均方根值和整流平均值都和振幅成正比,不過波形因數是二者相除,因此不受振幅的影響。一個特定的波形,若不失真的放大或縮小N倍,其波形因數不變。
均方根值計算時會用到訊號的平方,而整流平均值會用到訊號的絕對值,二者都不受正負號的影響。因此波形因數也不受正負號的影響,一個平均值為零的方波和其整流後的訊號,其波形因數相等。
波形因數是訊號的均方根值和整流平均值的比值,此外還有二個類似定義的因數:
- 峰值因數:,最大值和均方根值的比值。
- 平均因數:,最大值和整流平均值的比值,較少用到。
波形因數是三個因數中最小的一個:
由於他們的定義都和最大值、均方根值和整流平均值有關,三個因數間有以下的關係:
- ,[2]
因此也可以用峰值因數和平均因數來表示波形因數:
- .
特定波形的波形因數
若用表示波形的振幅,由於均方根值和整流平均值都和振幅成正比,二者對波形因數的影響恰好互相抵消,因此波形因數和振幅無關。像和的波形因數相等,因此可以用正規化,振幅為1的波形來計算波形因數。
| 波形 | 波形圖 | RMS | ARV | 波形因數 |
|---|---|---|---|---|
| 弦波 | 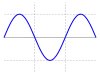 | [2] | [2] | [3] |
| 半波整流的弦波 | 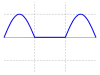 | |||
| 全波整流的弦波 | 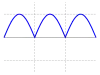 | |||
| 方波(占空比50%) | 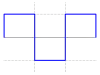 | |||
| 脈波 |  | [5] | ||
| 三角波 | 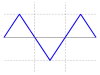 | [5] | ||
| 鋸齒波 | 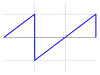 | |||
| 白雜訊 U(-1,1) |
參考資料
- Stutz, Michael. . BASIC AC THEORY. [30 May 2012]. (原始内容存档于2015-04-23).
- Dusza, Jacek; Grażyna Gortat, Antoni Leśniewski. . Warszawa: Wydawnictwo Politechniki Warszawskiej. 2002: 136–142, 197–203, 323. ISBN 83-7207-344-9 (波兰语).
- Jędrzejewski, Kazimierz. . Warsaw: Wydawnictwo Politechniki Warszawskiej. 2007: 86–87. ISBN 978-83-7207-4 (波兰语).
- Tanuwijaya, Franky. (PDF). Esco Micro Pte Ltd. [2012-12-13]. (原始内容存档 (PDF)于2019-07-13).
- Nastase, Adrian. . [9 June 2012]. (原始内容存档于2021-02-05).
外部連結
- RMS Calculator (页面存档备份,存于)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.