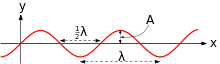
波矢
波向量是波的向量表示方法。波向量是一个向量,其大小表示波数(),其方向表示波传播的方向。
- 在這篇文章內,向量與标量分別用粗體與斜體顯示。例如,位置向量通常用 表示;而其大小則用 來表示。四維矢量用加有標號的斜體顯示。例如,或。為了避免歧意,四維矢量的斜體與標號之間不會有括號。例如,表示平方;而是的第二個分量。
波向量在狭义相对论背景下可定义为四维矢量。
定义

当波行进时,给定点的值以正弦作正弦振动。
狭义相对论
接近单色光的波包可以由波矢
准确描述,若明确的改写成共變和反變形式,则
- 且
- 。
於是波矢的大小为
最後一步等於零是因为对於真空中的光满足
洛伦兹变换
对波矢作洛伦兹变换可导出相對論性多普勒效應。洛伦兹矩阵定义为
- 。
在光被快速移动的波源激发的情况下,若要在地球坐标系(实验室坐标系)中检定光的频率,就要使用洛伦兹变换,如下所示。注意波源位於坐标系S s,地球位於观测系S obs。 对波矢进行洛伦兹变换得到
- 。
只考虑分量的情况,得到
- 。
其中是关於的方向余弦。
因此
波源远离观测者
当波源径直地远离观测者时,,方程变为:
- 。
波源接近观测者
当波源径直地接近观测者时,,方程变为:
- 。
参考文献
- Brau, Charles A. . Oxford University Press. 2004. ISBN 0-19-514665-4.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.