测地线
测地线(英语:Geodesic)又称大地线或短程线,数学上可视作直线在弯曲空间中的推广;在有度规定义存在之时,测地线可以定义为空间中两点的局域最短路径。测地线(英語:)的名字来自对于地球尺寸与形状的大地测量学(英語:)。
三維空間中的曲面
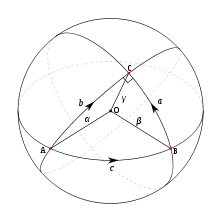
在大地线上,各点的主曲率方向均与该点上曲面法线相合。它在圆球面上为大圆弧,在平面上就是直线。在大地测量中,通常用大地线来代替法截线,作为研究和计算椭球面上各种问题。测地线是在一个曲面上,每一点处测地曲率均为零的曲线。
微分幾何的測地線
就稱之為測地線。其中是上的列維-奇維塔聯絡。方程左邊為曲線在流形上的加速度向量,所以方程是說測地線是在流形上加速度為零的曲線,也因此測地線必定是等速曲線。
以上方程用局部座標表示為
其中是的黎曼度量的克里斯托費爾符號。
唯一性及存在性
給定流形上一點及點上一個非零的切向量,因測地線方程是二階常微分方程,柯西-利普希茨定理指出存在區間,使得方程在此區間上存在唯一解
滿足初值條件,。但因為方程是非線性的,故未必在實數域上存在解。
從上述方程解的唯一性,可知若兩條測地線經過同一點,且在此點上有相同的切向量,則這兩條測地線是同一條測地線中的兩部份。
設是一條測地線,。如果對起點及起點的切向量改變得足夠細微,則存在新的測地線符合新的初值條件,且仍然定義在上。這個結果用嚴格語言敘述為:
- 給定測地線。在切叢中存在的一個鄰域,使得對任何,都存在測地線滿足初值條件。
從這結果可以得出,如果是定義在有界開區間上的測地線,對它的起點和此點上的切向量改變得足夠細微的話,則存在一條新的測地線滿足新的初值條件,並且定義在接近整條上。[1]
如果對於任意初始條件,都存在一條定義在整條實數線上的測地線,則稱是測地完備的。霍普夫-里諾定理指出,若是一個完備的度量空間,則是測地完備的。(上兩點間的度量,是連接此兩點的所有曲線的長度的最大下界。)
局部最短性
在黎曼流形上連接兩點之間的等速曲線,若其長度等於兩點間的距離,即這曲線是兩點間最短的曲線,那麼這曲線必定是測地線。然而,連接兩點間的測地線未必最短。比如在單位球面上,一條長度大於的測地線,不是連接這條線的兩端點間的最短曲線。因為球面上的測地線都是大圓的弧,若測地線長度大於,那麼測地線所在大圓上的另一條弧,其長度會小於,是連接這兩點的最短測地線。
連接兩點間最短測地線,也未必唯一。比如單位球面上兩個對徑點(即球面和一條直徑的兩個交點)之間,有無數條最短測地線相連。然而,流形上任何一點都存在一個鄰域,使得該點和鄰域上其他點之間,都有唯一的最短測地線相連(不計測地線的速度)。因此流形上任何測地線都是局部最短的。
對流形上一點,一條從出發的單位速的測地線,考慮所有的使得,即是說是一條最短測地線。這集合可以是或。若是前者,稱是沿著的割點,那麼對所有,是從點到的唯一最短測地線;若是後者,則對所有,都是點到的唯一最短測地線。沿著全部從出發的測地線的割點組成的集合,稱為的割迹。
度量幾何的測地線
一般的度量空間中,測地線是從區間的映射,使得對任何,都存在區間,使得包含在中一個開鄰域,並且對任何有
換言之,是連接其上任何兩點的一條最短路線。[2]
如果一個度量空間任何兩點都有測地線相連,稱為測地度量空間。
度量空間上的測地線的性質,和微分幾何有些不同:
兩條測地線即使有部分線段重合,卻未必屬於同一條測地線。例如在上定義度量(曼哈顿距离)
設是從(0,0)到(1,0)再到(1,1)的兩條線段所組成,而是從(0,0)到(2,0)的線段。這兩條都是測地線,且在(0,0)到(1,0)一段重合,但明顯不屬同一條測地線,因為這兩條線過了點(1,0)之後就分開。
一個測地度量空間中,在一點上未必存在一個鄰域,使得該點其鄰域其他點都有唯一的測地線。在上例的度量空間中,兩點間如果兩個座標都不同,則有無限多條測地線連接兩點。例如從(0,0)到(2,1),以下都是連接這兩點的最短測地線:任取一數,
就是先向右走到,再向上走到,再向右走到(2,1)。在任何一點的任何鄰域中,和該點兩個座標都不同的點有無數個,所以從該點到這些點之間,最短測地線都不是唯一。
參考
- Petersen, Peter (2006), Riemannian geometry, Graduate Texts in Mathematics, 171 (2nd ed.), Berlin, New York.
- Burago, Dmitri; Yuri Burago, and Sergei Ivanov (2001), A Course in Metric Geometry, American Mathematical Society.