海伦公式
(英語:),又譯希罗公式[1]、希倫公式。由古希臘數學家亞歷山大港的希羅發現,並在其於公元60年所著的《Metrica》中載有數學證明,原理是利用三角形的三條邊長求取三角形面積。亦有認為更早的阿基米德已經了解這條公式,因为《Metrica》是一部古代數學知識的結集,该公式的發現時間很有可能先於希羅的著作。[2]
假設有一個三角形,邊長分別為,三角形的面積可由以下公式求得:
- ,其中
中国南宋末年數學家秦九韶发现或知道等價的公式,其著作《數書九章》卷五第二题即三斜求积。“问沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里,里法三百步,欲知为田几何?”答曰:“三百十五顷.”其术文是:“以小斜幂併大斜幂,減中斜幂,餘半之,自乘於上;以小斜幂乘大斜幂,減上,餘四約之,爲實,一為從隅,開平方,得積。”若以大斜记为,中斜记为,小斜记为,秦九韶的方法相当于下面的一般公式:
- ,其中
像其他中國古代的數學家一样,他的方法沒有證明。根據现代數學家吴文俊的研究,秦九韶公式可由出入相補原理得出。
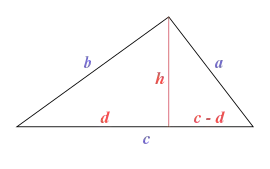
由於任何边的多邊形都可以分割成个三角形,所以海伦公式可以用作求多邊形面積的公式。比如说测量土地的面积的时候,不用测三角形的高,只需测两点间的距离,就可以方便地导出答案。
证明
用旁心來證明
設中,。
為內心,為三旁切圓。
四點共圓,並設此圓為圓。
- 過做鉛直線交於,再延長,使之與圓交於點。再過做鉛直線交於點。
- 先證明為矩形:,又(圓周角相等)。為矩形。因此,。
- 內切圓半徑,旁切圓半徑。且易知。由圓冪性質得到:。故
資料來源
- . [2009-07-06]. (原始内容存档于2009-06-16).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2009-07-06]. (原始内容存档于2015-09-05) (英语).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.