满射
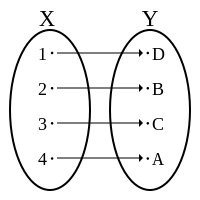
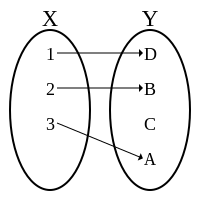
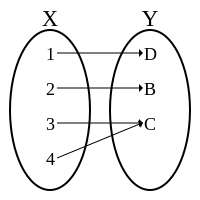
满射或蓋射(英語:),或稱满射函数或映成函數,一个函数为满射,則对于任意的陪域 中的元素 ,在函数的定义域 中存在一點 使得 。换句话说,是满射時,它的值域与陪域相等,或者,等价地,如果每一个陪域中的元素 其原像 不等於空集合。
| 各種函數 |
|---|
| x ↦ f (x) |
| 不同定義域和陪域 |
| 函數類/性質 |
| 構造 |
| 推廣 |
|
例子和反例
函数,定义为,不是一个满射,因为,(舉例)不存在一个实数满足。
但是,如果把的陪域限制到只有非负实数,则函数为满射。这是因为,给定一个任意的非负实数,我们能对求解,得到。
|
|
|
|
|
|
性质
若將定義在上的函數,視為其圖像,即(集合論經常如此行),則滿射與否,不僅是的性質,而是映射(需要聲明陪域)的性質。[1]單射與否可以單憑圖像判斷,但滿射則不同,不能單憑圖像判斷,因為要知道陪域。
右可逆函數
函數稱為函數的右逆,意思是對的所有元素成立。簡而言之,的效果,可以復原。用文字表示,是的右逆,意思是先做後做的複合,等於上的恆等函數,即不造成任何變化。此處不要求是的真正反函數,因為另一次序的複合,不必是的恆等函數。換言之,可以「復原」或「抵消」,但不必被復原或抵消。
若函數有右逆,則必為滿射。但反之,「每個滿射皆有右逆」此一命題,等價於選擇公理,故在某些集合論中(例如假設決定公理為真的集合論系統),不必為真。
右可消去
函數是滿射,當且僅當其為右可消去:[2]給定任何兩個有公共定義域和陪域的函數,若,則有。此性質的敍述用到函數和複合,可以對應推廣成範疇的態射和複合。右可消的態射稱為滿態射或滿同態。滿射與滿態射的關係在於,滿射就是集合範疇中的滿態射。
範疇論中,有右逆的態射必為滿態射,但反之則不然。態射的右逆也稱為的截面。而有右逆的態射稱為分裂滿態射,是一類特殊的滿態射。
作為二元關係
以為定義域,為值域的函數,可以視為兩集合之間的左全右唯一的二元關係,因為可將函數與圖像等同。此觀點下,由到的滿射,是右唯一而既左全又右全的關係。
定義域不小於陪域
滿射的定義域,必有大於或等於其陪域的基數:若為滿射,則的元素個數必定至少等於的元素個數(在基數意義下)。但此結論的證明,需要假定選擇公理,以證明有右逆,即存在函數使得對的任意元素成立。滿足此性質的必為單射,故由基數大小比較的定義,有。
特別地,若和皆是有限,且兩者的元素個數相同,則是滿射當且僅當為單射。
給定兩個集合和,以表示「或者為空,或者存在由至的滿射」。利用選擇公理,可以證明,和兩者一起,足以推出。此為康托爾-伯恩斯坦-施羅德定理的變式。
參考文獻
- Bourbaki, Nicolas. . Springer. 2004 [1968]. ISBN 978-3-540-22525-6.
- T. M. Apostol. . Addison-Wesley. 1981: 35.
- Goldblatt, Robert. [拓撲斯,邏輯的範疇論分析] Revised. Dover Publications. 2006 [1984] [2009-11-25]. ISBN 978-0-486-45026-1. (原始内容存档于2020-03-21) (英语).