無限階無限邊形鑲嵌
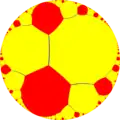
在幾何學中, 無限階無限邊形鑲嵌是一種雙曲面的正鑲嵌。其施萊夫利符號為{∞,∞}, 代表其有著無限個無限邊形圍繞於其所有的無窮遠點。
 龐加萊圓盤模型 | ||
| 類別 | 雙曲正鑲嵌 | |
|---|---|---|
| 對偶多面體 | 無限階無限邊形鑲嵌(自身對偶) | |
| 識別 | ||
| 鮑爾斯縮寫 | azazat | |
| 數學表示法 | ||
| 考克斯特符號 | ||
| 施萊夫利符號 | {∞,∞} | |
| 威佐夫符號 | ∞ | ∞ 2 ∞ ∞ | ∞ | |
| 組成與佈局 | ||
| 頂點圖 | ∞∞ | |
| 對稱性 | ||
| 對稱群 | [∞,∞], (*∞∞2) [(∞,∞,∞)] ,(*∞∞∞) | |
| 特性 | ||
| 點可遞、 邊可遞、 面可遞 | ||
| 圖像 | ||
| ||
對稱性
該鑲嵌的對偶鑲嵌代表*∞∞對稱性的基本域。
相關多面體與鑲嵌
該鑲嵌及其對偶鑲嵌的複合圖形能以正交的紅線及藍線區分。而其組合定義了*2∞2∞基本域的線。

- {∞,∞} 或
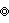



 =
= 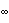
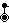
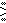
 ∪
∪ 

| [∞,∞] | ||||||
|---|---|---|---|---|---|---|
= = |
= = |
= = |
= = |
= = |
= |
= |
 |
 |
 |
 |
 |
 |
 |
| {∞,∞} | t{∞,∞} | r{∞,∞} | 2t{∞,∞}=t{∞,∞} | 2r{∞,∞}={∞,∞} | rr{∞,∞} | tr{∞,∞} |
| 對偶 | ||||||
 |
 |
 |
 |
 |
 |
 |
| V∞∞ | V∞.∞.∞ | V(∞.∞)2 | V∞.∞.∞ | V∞∞ | V4.∞.4.∞ | V4.4.∞ |
| 交錯 | ||||||
| [1+,∞,∞] (*∞∞2) |
[∞+,∞] (∞*∞) |
[∞,1+,∞] (*∞∞∞∞) |
[∞,∞+] (∞*∞) |
[∞,∞,1+] (*∞∞2) |
[(∞,∞,2+)] (2*∞∞) |
[∞,∞]+ (2∞∞) |
 |
 |
 |
 |
 |
 | |
| h{∞,∞} | s{∞,∞} | hr{∞,∞} | s{∞,∞} | h2{∞,∞} | hrr{∞,∞} | sr{∞,∞} |
| 交錯對偶 | ||||||
 |
 |
 |
 | |||
| V(∞.∞)∞ | V(3.∞)3 | V(∞.4)4 | V(3.∞)3 | V∞∞ | V(4.∞.4)2 | V3.3.∞.3.∞ |
| [(∞,∞,∞)] | ||||||
|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
| (∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) h2{∞,∞} |
(∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) h2{∞,∞} |
(∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) r{∞,∞} |
t(∞,∞,∞) t{∞,∞} |
| 對偶 | ||||||
 |
 |
 |
 |
 |
 |
 |
| V∞∞ | V∞.∞.∞.∞ | V∞∞ | V∞.∞.∞.∞ | V∞∞ | V∞.∞.∞.∞ | V∞.∞.∞ |
| 交錯 | ||||||
| [(1+,∞,∞,∞)] (*∞∞∞∞) |
[∞+,∞,∞)] (∞*∞) |
[∞,1+,∞,∞)] (*∞∞∞∞) |
[∞,∞+,∞)] (∞*∞) |
[(∞,∞,∞,1+)] (*∞∞∞∞) |
[(∞,∞,∞+)] (∞*∞) |
[∞,∞,∞)]+ (∞∞∞) |
 |
 |
 |
 |
 |
 |
 |
| 交錯對偶 | ||||||
 |
 |
 |
 |
 |
 |
|
| V(∞.∞)∞ | V(∞.4)4 | V(∞.∞)∞ | V(∞.4)4 | V(∞.∞)∞ | V(∞.4)4 | V3.∞.3.∞.3.∞ |
更高階數/邊數
即使無限階無限邊形已經達到雙曲鑲嵌的極限了,但仍可使用虛數來表示更高的邊數以及階數。
參考資料
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- . . Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
