环绕数

空间中任何两条闭曲线都恰好可以移动成如下标准位置之一。这决定了环绕数：

${\displaystyle \cdots }$
	环绕数 -2	环绕数 -1	环绕数 0
					${\displaystyle \cdots }$
		环绕数 1	环绕数 2	环绕数 3

每条曲线在移动过程中可以穿过自身，但这两条曲线保持互相分离。

六个正交叉与两个负交叉，这两条曲线的环绕数为 2。

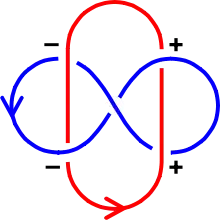
存在一个算法计算出一个链环图表的环绕数。按如下法则将每个交叉标记为“正”或“负” [1]：

正交叉数总数减去负交叉数总数等于环绕数的两倍，即

环绕数${\displaystyle ={\frac {n_{1}+n_{2}-n_{3}-n_{4}}{2}},\,}$

这里 n₁, n₂, n₃, n₄ 分别表示四类交叉数的个数。两个和 ${\displaystyle n_{1}+n_{3}\,\!}$ 与 ${\displaystyle n_{2}+n_{4}\,\!}$ 总相等[2]。这样得到了如下另外的公式

环绕数${\displaystyle =\,n_{1}-n_{4}\,=\,n_{2}-n_{3}.\,}$

注意到 ${\displaystyle n_{1}-n_{4}}$ 只涉及到蓝曲线被红曲线下交叉，而 ${\displaystyle n_{2}-n_{3}}$ 只涉及到上交叉。

怀特黑德链环两条曲线环绕数为零。

• 任何两条没有链接起来的曲线相交数为零。但环绕数为零的两条曲线仍可能是链接起来的（例如右图的怀特黑德链环）。
• 逆转任何一条曲线的定向，环绕数改变符号；但两条曲线同时逆转定向，环绕数不变。
• 环绕数具有手征性：取一个链环的镜像，环绕数改变符号。我们对正环绕数的约定基于右手法则。
• x-y 平面上一条定向曲线的卷绕数等于它与 z-轴（将 z-轴想象为三维球面中一条闭曲线）的环绕数。
• 更一般地，如果其中一条曲线是简单的，则这个分支的第一同调群同构于整数 Z。在此情形，环绕数由另一条曲线的同调类决定。
• 在物理学中，环绕数是拓扑量子数之一例，它与量子纠缠有关。

给定两条不交可微曲线 ${\displaystyle \gamma _{1},\gamma _{2}\colon S^{1}\rightarrow \mathbb {R} ^{3}}$，定义从环面到单位球面高斯映射 ${\displaystyle \Gamma }$ 为

${\displaystyle \Gamma (s,t)={\frac {\gamma _{1}(s)-\gamma _{2}(t)}{|\gamma _{1}(s)-\gamma _{2}(t)|}}.\,}$

取单位球面上一点 v，从而链环的正交投影到垂直于 v 的平面给出一个链环图表。观察到点 (s, t) 在高斯映射下映为 v 对应于链环图表中一个交叉，这里 ${\displaystyle \gamma _{1}}$ 在 ${\displaystyle \gamma _{2}}$ 上。并且 (s, t) 的一个邻域在高斯映射下映为 v 的一个邻域，保持或逆转定向取决于交叉的符号。从而为了计算这个对应于 v 的链环图表的环绕数，只需数高斯映射覆盖 v 的带符号次数。由于 v 是一个正则值，这恰是高斯映射的度数（即 Γ 的像盖住球面的带符号次数）。环绕数的同痕不变性自动由度数在同伦下不变得到。任何其它正则值将得到相同的数，所以环绕数与任何特定的链环图表无关。

曲线 γ₁ 与 γ₂ 的环绕数的这种表述给出了用二重线积分表示的一个明确公式，即高斯环绕积分：

环绕数${\displaystyle {}\,=\,\phi (\gamma _{1},\gamma _{2})={\frac {1}{4\pi }}\oint _{\gamma _{1}}\oint _{\gamma _{2}}{\frac {\mathbf {r} _{1}-\mathbf {r} _{2}}{|\mathbf {r} _{1}-\mathbf {r} _{2}|^{3}}}\cdot (d\mathbf {r} _{1}\times d\mathbf {r} _{2}).}$

这个积分求出了高斯映射像的全部带符号面积（被积函数是 Γ 的雅可比矩阵），然后除以球面的面积（等于 4π）。

• 就像三维中环绕的闭曲线，任何两个维数为 m 与 n 的闭流形，可能在 ${\displaystyle m+n+1}$ 维欧几里得空间中环绕起来。任何这样链环有一个相伴的高斯映射，其度数是环绕数的推广。
• 任何标架纽结有一个自环绕数，得自计算纽结 C 与将曲线 C 中的点沿着标架向量稍微移动得到一条新曲线的环绕数。由铅直移动（沿着黑板标架）得到的自环绕数称为考夫曼自环绕数（）。

U(1) 陳-西蒙斯理論是：

${\displaystyle CS={\frac {k}{4\pi }}\int _{M}AdA}$

若${\displaystyle M=R^{3}}$，路徑積分是

${\displaystyle Z(C_{1},C_{2})=\int dA\exp {(iCS+i\int _{C_{1}}A+i\int _{C_{2}}A)}=\int dA\exp {(iCS+i\int JA)}}$，

包括C1和C2的威爾森迴圈。J=J1+J2，而且

${\displaystyle J_{i}^{a}=\int _{C_{i}}dx^{a}\delta ^{3}(x-x_{i}(t))}$

因為這是高斯的積分，所以我們不需要重整化或正規化。再說這個積分是拓撲不變。

若J是经典方程就是

${\displaystyle dA=(2\pi /k)*J}$

或

${\displaystyle \nabla \times A=2\pi J/k}$

若我们选洛伦茨规范${\displaystyle d*A=0}$

${\displaystyle \nabla ^{2}A=-2\pi \nabla \times J/k}$

从电磁学，解是

${\displaystyle A(x)={\frac {1}{2k}}\int d^{3}y{\frac {\nabla \times J(y)}{|x-y|}}}$

则

${\displaystyle Z[C_{1},C_{2}]=\exp(2\pi i\phi (C_{1},C_{2})/k)}$

这是最简单的一个拓撲量子場論。根据爱德华·威滕的证明，非阿贝尔G的陈-西蒙斯论给其他拓扑不变，例如琼斯多项式。

• 陳-西蒙斯理論
• 卷绕数
• 绞拧数
• 扭转数
• 曲线的微分几何
• 链环 (纽结理论)
• 霍普夫不变量
• 吻接数

• A.V. Chernavskii, , Hazewinkel, Michiel (编), , Springer, 2001, ISBN 978-1-55608-010-4
• -, , Hazewinkel, Michiel (编), , Springer, 2001, ISBN 978-1-55608-010-4