瑞利-贝纳德对流

重力场中的对流原胞

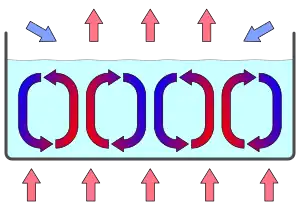
瑞利-贝纳德对流的特征可以通过法国物理学家亨利·贝纳德在1900年完成的一个简单实验来观察。

热传导特征

瑞利-贝纳德对流的电脑模拟

在瑞利-贝纳德对流中，对流原胞的旋转是稳定的，顺时针和逆时针的方向交替出现：这是自发对称破缺的一个实例。贝纳德原胞处于亚稳态，较小的扰动不会改变原胞的旋转，而较大的则会有影响。这也是某种形式的迟滞现象的表现。

另外在模拟的过程中也发现，微观层面上具有决定性的定律，在宏观层面上却造成了非决定性的结果。对初态进行微观层面上的扰动足以产生非决定性的宏观效应。某个微观扰动在宏观上产生的效应是无法计算的，这也是复杂系统（complex system）的特征之一（即蝴蝶效应）。如果进一步提升液体底部的温度，之前形成的湍流会变得混沌起来。

对流的贝纳德原胞趋向于形成规则的正六角棱柱，特别是在没有过分扰动的情况下[5][6]；在某些实验条件下，原胞也会出现正四棱柱[7]或螺旋状[8]。

贝纳德原胞常出现在由表面张力驱动的对流中。一般来说，瑞利和皮尔森的分析[9]（线性理论）的解导致了简并的出现。若考虑实际的系统，对流图案则取决于系统边界的形状。

由于液体的上表面和下表面之间有密度梯度，重力会使较冷的、密度较大的液体向下运动，而此运动会受到液体粘性阻尼的阻扰。两股作用力的平衡可以由一个无量纲的参数（瑞利数）来表示。此处的瑞利数定义如下：

${\displaystyle \mathrm {Ra} _{L}={\frac {g\beta }{\nu \alpha }}(T_{b}-T_{u})L^{3}}$

其中

T_u 表示液体上表面的温度；

T_b 表示液体下表面的温度；

L 表示容器的高度；

g 表示重力加速度；

ν 表示黏度；

α 表示热扩散率；

β 表示热膨胀系数。

随着瑞利数的增大，重力在系统中的影响越大。系统在临界瑞利数1708[2]时开始不稳定，出现对流原胞。

在某稳定系统中通过对线性化的方程进行微扰分析，可获得某些边界条件下的临界瑞利数[10]。最简单情况的是两条自由的边界（即瑞利男爵在1916年解出的情况[11]），得到的瑞利数 Ra = ²⁷⁄₄ π⁴ ≈ 657.51[12]。对于刚性的底部和自由的顶部边界条件（对应着无盖的水壶），则有临界瑞利数 Ra = 1,100.65[13]。

若液体上表面与空气接触，浮力和表面张力也会参与对流图案的形成。由于馬倫哥尼效應，液体趋向于流向表面张力较强的区域。升高温度会降低液体的表面张力，导致液体从较热的区域流向较冷的区域[14]。为了保持液面水平，较冷的液体将会下降，这也成为了对流原胞形成的驱动力之一。这一类由温度梯度驱动的特殊例子被称为热毛细对流（thermo-capillary convection）或贝纳德-马伦哥尼对流（Bénard–Marangoni convection）。

瑞利男爵是最早对瑞利-贝纳德对流进行成功的理论分析的科学家，他假设的边界条件是：在上下表面边界，流体速度在竖直方向上的分量为零，且没有温度干扰。这些假设令他的分析与亨利·贝纳德的实验相左。之后，皮尔森基于对表面张力的考虑，重新对贝纳德的实验进行了分析[9]。虽然如此，现今用“瑞利-贝纳德对流”指代温度造成的效应，而用“贝纳德-马伦哥尼对流”指代表面张力造成的效应[1]。Davis 和 Koschmieder 建议将瑞利-贝纳德对流正名为“皮尔森-贝纳德对流”[2]。

• 流体动力稳定性
• 馬倫哥尼效應
• 自然对流
• 巨人堤道

• Subrahmanyan Chandrasekhar (1982). Hydrodynamic and Hydromagnetic Stability (Dover). ISBN 0-486-64071-X
• P.G. Drazin and W.H. Reid (2004). Hydrodynamic Stability, second edition (Cambridge University Press).
• A.V. Getling (1998). Rayleigh-Bénard Convection: Structures and Dynamics (World Scientific). ISBN 9810226578
• E.L. Koschmieder (1993). Bénard Cells and Taylor Vortices (Cambridge University Press). ISBN 0-521-40204-2
• B. Saltzman (ed., 1962). Selected Papers on the Theory of Thermal Convection, with Special Application to the Earth's Planetary Atmosphere (Dover).
• R. Kh. Zeytounian (2009). Convection in Fluids: A Rational Analysis and Asymptotic Modelling (Springer).

维基共享资源上的相关多媒体资源：瑞利-贝纳德对流

• A. Getling, O. Brausch: Cellular flow patterns （页面存档备份，存于）
• K. Daniels, B. Plapp, W.Pesch, O. Brausch, E. Bodenschatz: Undulation Chaos in inclined Layer Convection
• Karen E. Daniel, Oliver Brausch, Werner Pesch, Eberhard Bodenschatz: Competition and bistability of ordered undulations and undulation chaos in inclined layer convection （页面存档备份，存于） (PDF; 608 kB)
• P. Subramanian, O. Brausch, E. Bodenschatz, K. Daniels, T.Schneider W. Pesch: Spatio-temporal Patterns in Inclined Layer Convection （页面存档备份，存于） (PDF; 5,3 MB)