生日問題

生日問題可理解成盲射打靶问题。首先計算：23人皆不同生日的概率是多少？可想像一間有23人進入的房間，這23人依次進入，每個進入的人的生日都與房裏其他人的生日不同的概率依次是1、${\textstyle {\frac {364}{365}}}$、${\textstyle {\frac {363}{365}}}$、${\textstyle {\frac {362}{365}}}$、${\textstyle {\frac {361}{365}}}$等。先入房的人的生日皆不同的概率很高，前五个是1×${\textstyle {\frac {364}{365}}}$×${\textstyle {\frac {363}{365}}}$×${\textstyle {\frac {362}{365}}}$×${\textstyle {\frac {361}{365}}}$=97.3%；而最后入房的几人就完全不同，他們入房且找不到同生日者的概率是${\textstyle {\frac {345}{365}}}$、${\textstyle {\frac {344}{365}}}$、${\textstyle {\frac {343}{365}}}$。这种概率可看成对靶的盲射：靶有365格，其中17个左右黑格，其余白格。假设每枪必中靶并且分布符合几何概型的话，连射12枪左右任何一发都没有击中黑格的概率（投射于房间里的人生日皆不同）十分微小。

理解生日問題的关键在于考虑上述“依次入房”模型中最后几个入房的人“全都没碰到同生日的人”概率多少。

简言之，大多数人之所以会认为23人中兩人同生日的概率应该远远小于50%，是因为将问题理解为“其他22人与你同生日的概率”，而非问题真諦“23人中两两之间存在生日相同”。如果有考虑这点，直觉上会将原来的概率乘以23（注意：此算法并不正确），则会意识到概率很大。

假設有n個人在房內，如果要計算兩人同生日的機率，在不考慮特殊因素如閏年、雙胞胎的前提下，假設一年365日出生概率平均分佈（現實的出生機率不是平均分佈）。

計算概率的方法是，首先找出p（n）表示n人中，每人生日都不同的概率。假如n > 365，根據鴿巢原理其概率為0，假设n ≤ 365，则概率为

${\displaystyle {\bar {p}}(n)=1\cdot \left(1-{\frac {1}{365}}\right)\cdot \left(1-{\frac {2}{365}}\right)\cdots \left(1-{\frac {n-1}{365}}\right)={\frac {365}{365}}\cdot {\frac {364}{365}}\cdot {\frac {363}{365}}\cdot {\frac {362}{365}}\cdots {\frac {365-n+1}{365}}}$

该图片显示特定人数对应的2个人生日一样的概率

因为第二人不能跟第一人同生日（概率是364/365），第三人不能跟前两人同生日（概率是363/365），依此类推。用阶乘可写成如下形式

${\displaystyle {365! \over 365^{n}(365-n)!}}$

p(n）表示n个人中至少兩人同生日的概率

${\displaystyle p(n)=1-{\bar {p}}(n)=1-{365! \over 365^{n}(365-n)!}}$

n≤365，根据鸽巢原理，n大于365时概率为1。

n是23時概率约0.507。其他人數的概率用上面算法可得出：

比较p (n) = 任意两人同生日的概率；q (n) =和某人同生日的概率

注意所有人都是随机选出：作为对比，q(n)表示房间中有n+1人，當中与特定人（比如你）同生日的概率：

${\displaystyle q(n+1)=1-\left({\frac {364}{365}}\right)^{n}}$

当n = 22时概率只有大约0.059，约高于十七分之一。如果n人中有50％概率存在某人跟你同生日，n至少要达到253。注意这数字大大高于365/2 = 182.5；究其原因是因为房间内可能有些人同生日。

保羅·哈莫斯在自传中认为生日問題只用计算数值来解释是种悲哀，所以给出了一种概念数学方法的解释（尽管这方法有一定的误差）：乘积

${\displaystyle \prod _{k=1}^{n-1}\left(1-{k \over 365}\right)}$

等于1－p（n），因此关注第一个n，欲使乘积小于1/2。由平均数不等式可知：

${\displaystyle {\sqrt[{n-1}]{\prod _{k=1}^{n-1}\left(1-{k \over 365}\right)}}<{1 \over n-1}\sum _{k=1}^{n-1}\left(1-{k \over 365}\right)}$

再用已知的1到n－1所有整数和等于n（n－1）/2，然后用不等式1－x < e^−x，可得到：

${\displaystyle \prod _{k=1}^{n-1}\left(1-{k \over 365}\right)<\left({1 \over n-1}\sum _{k=1}^{n-1}\left(1-{k \over 365}\right)\right)^{n-1}}$

${\displaystyle =\left(1-{n \over 730}\right)^{n-1}<\left(e^{-n/730}\right)^{n-1}=e^{-(n^{2}-n)/730}}$

如果仅当

${\displaystyle n^{2}-n>730\log _{e}2\cong 505.997\dots }$

最后一條表达式的值会小于0.5。其中log_e表示自然对数，略小于506，如果取n²－n=506就得到n＝23。

在推导中，哈莫斯写道：

这推論是基于数学系学生必须掌握的重要工具。生日问题曾是用来演示纯思维如何胜过机械计算的绝妙例子：这些不等式一两分钟就写得出，但乘法运算就要更多时间且更易出错，无论使用的工具是铅笔还是老式电脑。计算器不能提供的是理解力、数学才能、或产生更高级、普适化理论的坚实基础。[1]

然而哈莫斯的推論只显示至少超過23人就能保证平等机会下的生日匹配。因为不知道给出的不等式有多強（嚴格、清晰），因此無法藉此計算過程確定n＝22是否能讓機率過半；相反，現在任何人都可用Microsoft Excel等個人電腦程式在幾分鐘內把整幅機率分佈圖畫出來，對問題答案很快就有通盤掌握，一目了然。

用公式${\displaystyle p(n)\sim 1-1/\exp(n^{2}/(2N))}$（紅綫）與真實概率（黑綫）的比較

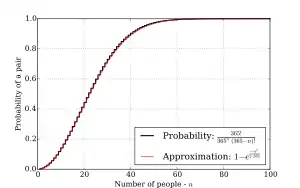
生日問題可以推广一下：假设有n人，每人都随机从N个特定的数中选一个数出来（N可能是365或其他正整数）。

p（n）表示有两个人选择了同样的数字，这概率多大?

下面的逼近公式可以回答这个问题

${\displaystyle p(n)\sim 1-1/\exp(n^{2}/(2N))}$。

反算问题可能是：

对于确定的概率p…

…找出最大的n（p）满足所有的概率p（n）都小于给出的p，或者

…找出最小的n（p）满足所有的概率p（n）都大于指定的p。

这问题有如下逼近公式：

${\displaystyle n(p)\approx {\sqrt {2\cdot 365\ln \left({1 \over 1-p}\right)}}+{1 \over 2}}$。

生日問題可以用计算机代码经验性模拟

days := 365;
numPeople := 1;
prob := 0.0;
while prob < 0.5 begin
    numPeople := numPeople + 1;
    prob := 1 -((1-prob)*(days-(numPeople-1)) / days);
    print "Number of people: " + numPeople;
    print "Prob. of same birthday: " + prob;
end;

生日問題也可以用Microsoft Excel Spreadsheet模拟

当行数达到23（即人数），可看到概率结果开始過半。

生日問題普遍的应用于检测哈希函数：N-位长度的哈希表可能发生碰撞测试次数不是2^N次而是只有2^N/2次，这结论用在破解密码学散列函数的生日攻击中。

生日问题隐含的理论已经在[Schnabel 1938]名字叫做捉放法（capture-recapture）的统计试验得到应用，来估计湖的鱼数。

就像上面提到的，現实世界人口的生日并非平均分佈，这种非均衡生日概率问题也已解决。

此问题的另外一个泛化是求在n人中有两人的生日同在k日历天内的概率。假设有m个同等可能的生日。[2]

${\displaystyle {\begin{aligned}p(n,k,m)&=1-{\frac {(m-nk-1)!}{m^{n-1}{\bigl (}m-n(k+1){\bigr )}!}}\end{aligned}}}$

能找到两个人生日相差k天或更少的概率高于50%所需要的人数：

k	n for m = 365
0	23
1	14
2	11
3	9
4	8
5	8
6	7
7	7

只須随机抽取7人，找到两人生日相差一周内的概率就会過半。[2]

星期二男孩問題：一個兩孩家庭有一個男孩，他是星期二出生的，那麼另一個孩子也是男孩的機率是多少？答：13/27[3]

• Zoe Emily Schnabel: "The estimation of the total fish population of a lake"（某湖中鱼类总量估计），美国数学月刊45（1938年）, 348-352页
• M. Klamkin，D. Newman: "Extensions of the birthday surprise"（生日惊喜的扩充）, Journal of Combinatorial Theory 3（1967年）,279-282页。
• D. Blom: "a birthday problem"生日问题，美国数学月刊80（1973年）,1141-1142页。这一论文证明了当生日按照平均分布，两个生日相同的概率最小。

• 概率论
• 生日
• 生日攻击
• 哈希函数

• http://www.efgh.com/math/birthday.htm （页面存档备份，存于）
• http://www.teamten.com/lawrence/puzzles/birthday_paradox.html （页面存档备份，存于）
• http://science.howstuffworks.com/question261.htm （页面存档备份，存于）
• http://mathworld.wolfram.com/BirthdayProblem.html （页面存档备份，存于）
• http://www.atriumtech.com/pongskorn/birthdayparadox/birthdayparadox.htm （页面存档备份，存于）