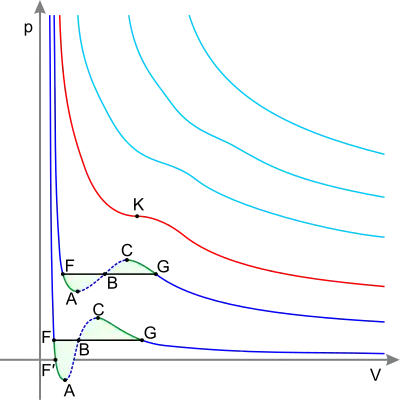
實際氣體

${\displaystyle RT=(P+{\frac {a}{V_{m}^{2}}})(V_{m}-b)}$

对于上式，a是同分子引力有关的常数，b是同分子自身体积有关的常数，统称为范德华常数，V_m为气体的摩尔体积，p是气体的压强，V是气体的体积，T为热力学温度，R=8.314J·mol^-1·K^-1

雷德利希-邝氏方程是另一个实际气体二元方程。比 范德华方程更精确，同时比大多数多元实际气体方程精确。

${\displaystyle RT=P(V_{m}-b)+{\frac {a}{V_{m}(V_{m}+b)T^{\frac {1}{2}}}}(V_{m}-b)}$

• ${\displaystyle \ a}$ 为常数，用于修正分子间引力；
• ${\displaystyle \ b}$ 为常数，用于修正体积。

注意这里的常数a，b与范德华方程中的不同。 ${\displaystyle a=0.4275{\frac {R^{2}T_{c}^{2.5}}{P_{c}}}}$

${\displaystyle b=0.0867{\frac {RT_{c}}{P_{c}}}}$

贝特罗方程[1]极少使用。

${\displaystyle P={\frac {RT}{V_{m}-b}}-{\frac {a}{TV_{m}^{2}}}}$

修正式更为精确：

${\displaystyle P={\frac {RT}{V_{m}}}\left[1+{\frac {9P/P_{c}}{128T/T_{c}}}\left(1-{\frac {6}{(T/T_{c})^{2}}}\right)\right]}$

狄特里奇方程近年来亦很少使用。 ${\displaystyle P=RT{\frac {\exp {({\frac {-a}{V_{m}RT}})}}{V_{m}-b}}}$.

克劳修斯方程是非常简洁的三元实际气体方程。

${\displaystyle RT=\left(P+{\frac {a}{T(V_{m}+c)^{2}}}\right)(V_{m}-b)}$

其中

${\displaystyle a={\frac {27R^{2}T_{c}^{3}}{64P_{c}}}}$

${\displaystyle b=V_{c}-{\frac {RT_{c}}{4P_{c}}}}$

${\displaystyle c={\frac {3RT_{c}}{8P_{c}}}-V_{c}}$

维里方程 ${\displaystyle PV_{m}=RT\left(1+{\frac {B(T)}{V_{m}}}+{\frac {C(T)}{V_{m}^{2}}}+{\frac {D(T)}{V_{m}^{3}}}+...\right)}$

或

${\displaystyle PV_{m}=RT\left(1+{\frac {B^{\prime }(T)}{P}}+{\frac {C^{\prime }(T)}{P^{2}}}+{\frac {D^{\prime }(T)}{P^{3}}}+...\right)}$

其中 A, B, C, A′, B′, C′ 是温度依赖常数。

${\displaystyle P={\frac {RT}{V_{m}-b}}-{\frac {a(T)}{V_{m}(V_{m}+b)+b(V_{m}-b)}}}$

${\displaystyle RT=\left(P+{\frac {a}{TV_{m}(V_{m}-b)}}-{\frac {c}{T^{2}V_{m}^{3}}}\right)(V_{m}-b)}$

其中

${\displaystyle a=6P_{c}T_{c}V_{c}^{2}}$

${\displaystyle b={\frac {V_{c}}{4}}}$

${\displaystyle c=4P_{c}T_{c}^{2}V_{c}^{3}}$.

${\displaystyle P={\frac {RT}{v^{2}}}\left(1-{\frac {c}{vT^{3}}}\right)(v+B)-{\frac {A}{v^{2}}}}$

其中

${\displaystyle A=A_{0}\left(1-{\frac {a}{v}}\right)}$

${\displaystyle B=B_{0}\left(1-{\frac {b}{v}}\right)}$

这个方程在密度0.8 ρ_cr以下时较为精确, 其中 ρ_cr是物质的临界点密度。 方程中的常数如下表所列： P的单位是kPa, V的单位是${\displaystyle {\frac {m^{3}}{Kmol}}}$, R=8.314${\displaystyle {\frac {kPa.m^{3}}{Kmol.K}}}$[3]

BWR方程

${\displaystyle P=RTd+d^{2}\left(RT(B+bd)-(A+ad-a{\alpha }d^{4})-{\frac {1}{T^{2}}}[C-cd(1+{\gamma }d^{2})\exp(-{\gamma }d^{2})]\right)}$

其中d是摩尔密度； a, b, c, A, B, C, α, γ 是经验常数。