等角共轭
几何学中,设点 P 是三角形 ABC 平面上一点,作直线 PA、PB 和 PC 分别关于角 A 、B 和 C 的平分线的反射,这三条反射线必然交于一点[1],称此点为 P 关于三角形 ABC 的等角共轭。(这个定义只对点,不是对三角形 ABC 的边。)
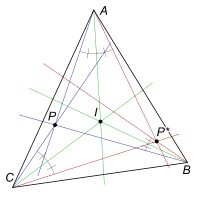
点 P 的等角共轭
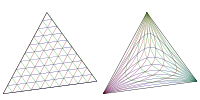
三角形内部点的等角共轭变换
点 P 的等角共轭点经常记作 P*,显然 P*的等角共轭点即为 P。
内心 I 的等角共轭点是自身。垂心 H 的等角共轭点是外心 O。重心的等角共轭点是类似重心 K。
在三线坐标中,如果 X = x : y : z 是不在三角形 ABC 边上的一点,那么它的等角共轭是 1/x : 1/y : 1/z。因此,X 的等角共轭有时也记作 X −1。三角形内部的点集 S 在三线乘法
- (p : q : r) * (u : v : w) = pu : qv : rw,
下构成一个交换群。S 中任何一点 X 的逆是 X −1。
因为等角共轭是一个函数,从而我们可以讨论一个点集的等角共轭。譬如,直线的等角共轭是一条外接圆锥曲线;确切的,若直线交外接圆于 0、1或 2 点,其等角共轭分别为椭圆、抛物线或双曲线。外接圆的等角共轭是无穷远直线。一些有名的三次曲线(例如:Thompson 三次曲线、Darboux 三次曲线、Neuberg 三次曲线)是自等角共轭的,即如果 X 位于这些三次曲线上,那么X −1 也在其上。
注释和参考
- 可以用塞瓦定理的逆定理证明。
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.