線性化

函数的線性化為線性函數。針對函數${\displaystyle y=f(x)}$，若要用在任意點${\displaystyle x=a}$下的值及其圖形斜率來進行近似時，假設${\displaystyle f(x)}$在${\displaystyle [a,b]}$（或${\displaystyle [b,a]}$）區間內可微，且b鄰近a，線性化是可以有效近似的方法。簡單來說，線性化就是在${\displaystyle x=a}$點附近，以直線來近似函數的值。例如${\displaystyle {\sqrt {4}}=2}$，那麼針對${\displaystyle {\sqrt {4.001}}={\sqrt {4+.001}}}$，利用線性化就可能可以找到理想的近似公式。

針對任意函數${\displaystyle y=f(x)}$，${\displaystyle f(x)}$在已知可微分點附近的位置，都可以被近似。最基本的要求是${\displaystyle L_{a}(a)=f(a)}$，其中${\displaystyle L_{a}(x)}$是${\displaystyle f(x)}$在${\displaystyle x=a}$的線性化。一次方程的圖形會形成直線，例如通過點 ${\displaystyle (H,K)}$，斜率為${\displaystyle M}$為直線。方程式的一般形為${\displaystyle y-K=M(x-H)}$。

若是配合點${\displaystyle (a,f(a))}$，${\displaystyle L_{a}(x)}$即變成${\displaystyle y=f(a)+M(x-a)}$。因為可微分函數是局部線性，該點的斜率可以用${\displaystyle f(x)}$在點${\displaystyle x=a}$切線的斜率來代替。

函數局部線性的意思也表示函數圖形上的點可以任意接近點${\displaystyle x=a}$，相對來說比較接近的點，其線性近似的效果也會比較好。斜率${\displaystyle M}$最準確的值會是在${\displaystyle x=a}$點的切線斜率。

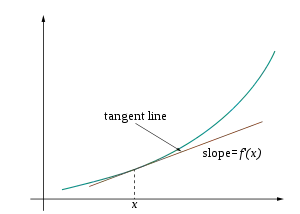
f(x)=x^2在(x, f(x))的近似值

旁邊的圖可以說明${\displaystyle f(x)}$在點${\displaystyle x}$的切線。在${\displaystyle f(x+h)}$位置，其中${\displaystyle h}$是小的正值或是負值，${\displaystyle f(x+h)}$非常接近${\displaystyle (x+h,L(x+h))}$點的切線。

函數在點${\displaystyle x=a}$線性化的最終方程為：

${\displaystyle y=(f(a)+f'(a)(x-a))}$

針對${\displaystyle x=a}$，${\displaystyle f(a)=f(x)}$。函數${\displaystyle f(x)}$的導數為${\displaystyle f'(x)}$，而函數${\displaystyle f(x)}$在點${\displaystyle a}$的斜率為${\displaystyle f'(a)}$。

若要找${\displaystyle {\sqrt {4.001}}}$，可以用${\displaystyle {\sqrt {4}}=2}$的資訊。函數${\displaystyle f(x)={\sqrt {x}}}$在點${\displaystyle x=a}$的線性化為${\displaystyle y={\sqrt {a}}+{\frac {1}{2{\sqrt {a}}}}(x-a)}$，因為函數${\displaystyle f'(x)={\frac {1}{2{\sqrt {x}}}}}$定義了函數${\displaystyle f(x)={\sqrt {x}}}$在點${\displaystyle x}$的斜率。

代入${\displaystyle a=4}$，其線性化結果為${\displaystyle y=2+{\frac {x-4}{4}}}$。

針對${\displaystyle x=4.001}$的例子，可得${\displaystyle {\sqrt {4.001}}}$近似${\displaystyle 2+{\frac {4.001-4}{4}}=2.00025}$。其實際值為2.00024998，非常接近，此線性化的誤差小於1%的百萬分之一。

函數${\displaystyle f(x,y)}$在點${\displaystyle p(a,b)}$線性化的方程式為：

${\displaystyle f(x,y)\approx f(a,b)+\left.{\frac {\partial f(x,y)}{\partial x}}\right|_{a,b}(x-a)+\left.{\frac {\partial f(x,y)}{\partial y}}\right|_{a,b}(y-b)}$

多變數函數${\displaystyle f(\mathbf {x} )}$在點${\displaystyle \mathbf {p} }$線性化的通式為

${\displaystyle f({\mathbf {x} })\approx f({\mathbf {p} })+\left.{\nabla f}\right|_{\mathbf {p} }\cdot ({\mathbf {x} }-{\mathbf {p} })}$

其中${\displaystyle \mathbf {x} }$是變數向量，而${\displaystyle \mathbf {p} }$是要線性化的點[2]。

配合線性化的技術，可以用研究線性系統的工具來分析非線性系統在特定點附近的行為。函數在特定點附近的線性化是在該點附近泰勒级数的一階展開。針對以下的系統

${\displaystyle {\frac {d\mathbf {x} }{dt}}=\mathbf {F} (\mathbf {x} ,t)}$,

其線性化系統為

${\displaystyle {\frac {d\mathbf {x} }{dt}}\approx \mathbf {F} (\mathbf {x_{0}} ,t)+D\mathbf {F} (\mathbf {x_{0}} ,t)\cdot (\mathbf {x} -\mathbf {x_{0}} )}$

其中${\displaystyle \mathbf {x_{0}} }$是要觀測的特定點，而${\displaystyle D\mathbf {F} (\mathbf {x_{0}} )}$是${\displaystyle \mathbf {F} (\mathbf {x} )}$在點${\displaystyle \mathbf {x_{0}} }$所計算的雅可比矩阵。

• 線性穩定性
• 切線剛性矩陣
• 穩定性導數
• 泰勒公式
• 泛函方程 (L函數)

• Linearization for Model Analysis and Control Design （页面存档备份，存于）