线性代数基本定理
线性代数基本定理是秩为 r 的 m×n 矩阵A的奇异值分解:
对于矩阵 (有行及列)产生了四个基本线性子空间:
| 子空间名字 | 定义 | 包含于 | 维数 | 基 |
|---|---|---|---|---|
| 列空间、值域或像 | 或 | 的前 列 | ||
| 左零空间或上核 | 或 | 的后 列 | ||
| 行空间或余象 | 或 | 的前 列 | ||
| 零空间或核 | 或 | 的后 列 |
Secondly:
- In , , 也就是, 零空间与行空间的正交补相同.
- In , , 也就是, 左零空间为列空间的正交补.
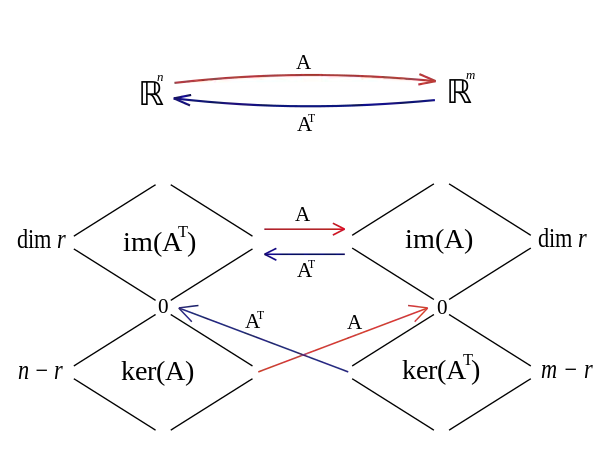
矩阵A的四个基本子空间.
子空间的维数遵从秩-零化度定理.
进一步, 所有这些空间本质地定义于– 不必考虑基的选择 – 抽象向量空间, 算子, 对偶空间 与: 的核与像是的上核与余象.
参考文献
- Strang, Gilbert. Linear Algebra and Its Applications. 3rd ed. Orlando: Saunders, 1988.
- Strang, Gilbert, (PDF), American Mathematical Monthly, 1993, 100 (9): 848–855, JSTOR 2324660, doi:10.2307/2324660
外部链接
- Gilbert Strang, MIT Linear Algebra Lecture on the Four Fundamental Subspaces (页面存档备份,存于), from MIT OpenCourseWare
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.