薄膜生长模式
薄膜生长模式(Modes of thin-film growth)指的是薄膜在材料表面的外延成长中不同的生长机制,由恩斯特·鲍尔于1958年系统化地归纳为三大类型[1]:岛状生长模式(即Volmer-Weber模式)、层状生长模式(即Frank–van der Merwe模式)和岛状/层状生长模式(即斯特兰斯基-克拉斯坦诺夫模式)[注 1]。
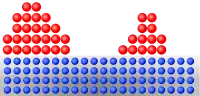

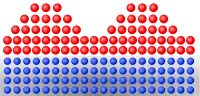

基本生长模式
岛状生长模式
岛状生长模式又称Volmer-Weber模式、VM模式,得名于马克斯·福尔默和A. 韦伯[4]。在岛状生长中,薄膜原子相互之间的束缚力强于衬底对薄膜原子的束缚力,导致薄膜原子在衬底表面直接成核生长出三维的原子岛[5]。大部分薄膜都是呈岛状生长的[6]。
理论解释
不同的薄膜生长模式取决于薄膜和衬底材料表面的化学与物理性质,例如表面张力和晶格系数[11][12][5],可通过考虑距离表面最近的几层原子的化学势来确定生长机制[12][13]。1995年,伊万·马尔可夫提出原子层内单原子的化学势模型[13]:
其中 表示吸附材料的体化学势(bulk chemical potential), 表示浸润层吸附原子的脱附能(desorption energy), 表示衬底吸附原子的脱附能, 表示每个原子的位错错配能(misfit dislocation energy), 表示每个原子的同质应变能(homogeneous strain energy)。在一般情况下,、、 和 的值与薄膜的厚度,以及衬底和薄膜之间的位错有着极为复杂的关系。在应变很小的情况下(即 ),薄膜的生长模式取决于 的值:
实验测量
在实际的科学实验中,可以运用多种手段判断薄膜生长的模式,包括透射电子显微镜或扫描隧道显微镜(直接测量表面形貌),低能电子衍射或反射式高能电子衍射(通过测量衍射强度的振荡),以及俄歇电子能谱[5]。
参考文献
- Bauer, Ernst. . Zeitschrift für Kristallographie. 1958, 110: 372–394. Bibcode:1958ZK....110..372B. doi:10.1524/zkri.1958.110.1-6.372.
- 江绍基. (PDF). 中山大学. [2017-10-13]. (原始内容存档 (PDF)于2017-10-14).
- . (PDF). . 2007-03, 6 (1): 64.
- Volmer, M.; Weber, A. . Z. Phys. Chem. 1926, 119: 277–301.
- Oura, K.; V.G. Lifshits; A.A. Saranin; A.V. Zotov; M. Katayama. . Berlin: Springer. 2003. ISBN 3-540-00545-5.
- . SHINCRON Co.,Ltd. [2017-10-13]. (原始内容存档于2016-09-13).
- Frank, F. C.; van der Merwe, J. H. . Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 198 (1053): 205–216. Bibcode:1949RSPSA.198..205F. JSTOR 98165. doi:10.1098/rspa.1949.0095.
- Frank, F. C.; van der Merwe, J. H. . Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 198 (1053): 216–225. Bibcode:1949RSPSA.198..216F. JSTOR 98166. doi:10.1098/rspa.1949.0096.
- Frank, F. C.; van der Merwe, J. H. . Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1949, 200 (1060): 125–134. Bibcode:1949RSPSA.200..125F. JSTOR 98394. doi:10.1098/rspa.1949.0163.
- Stranski, I. N.; Krastanov, L. . Sitzungsber. Akad. Wiss. Wien. Math.-Naturwiss. 1938, 146: 797–810.
- Venables, John. . Cambridge: Cambridge University Press. 2000. ISBN 0-521-62460-6.
- Pimpinelli, Alberto; Jacques Villain. . Cambridge: Cambridge University Press. 1998. ISBN 0-521-55198-6.
- Markov, Ivan V. . Singapore: World Scientific. 1995. ISBN 981-02-1531-2.