虛功
在分析力學裏,施加於某物體的作用力,由於給定的虛位移,所做的機械功,稱為虛功(英語:)。以方程式表達,虛功是
- ;
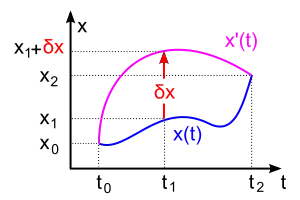
粒子的運動軌道與虛軌道分別為與。在位置、時間,虛位移為。兩種軌道的初始位置與終止位置分別為與。
其中,是作用力,是虛位移。
在這篇文章裏,位移指的是平移運動所造成的位移或旋轉運動所造成的角位移;作用力指的是力量或力矩。虛位移不是實際的位移,而是一種虛構的、理論上的位移,是一種只涉及位置,不涉及時間的變化。每一個虛位移既是自變量(),又是任意設定的。任意性是一個很重要的特性,在數學關係式裏,能夠推導出許多重要的結果。例如,思考下述矩陣方程式:
- ;
其中,都是向量,是方塊矩陣。
假若,是個任意非零向量,則可以將任意項目從方程式中除去,得到。
虛功原理
虛功原理闡明,一個物理系統處於靜態平衡(),若且唯若,所有施加的外力,經過符合約束條件的虛位移,所做的虛功的總和等於零[1][2]。以方程式表達,
- 。
考慮一個由一群質點組成,呈靜態平衡的物理系統,其內部任意一個質點可能感受到很多個作用力。這些作用力的總和等於零:
- 。
給予這質點 虛位移,則合力所做的虛功為零:
- 。
總合這系統內做於每一個質點的虛功,其答案也是零:
- 。
將合力細分為外力與約束力:
- 。
假設所有約束力所做的符合約束條件的虛功,其總合是零[3]:
- ,
則約束力項目可以從方程式中除去,從而得到虛功原理的方程式:
- 。
注意到這推論裏的約束力假設。在這裏,約束力就是牛頓第三定律的反作用力。因此,可以稱此假設為反作用力的虛功假設:所有反作用力所做的符合約束條件的虛功,其總合是零。這是分析力學額外設立的假設,無法從牛頓運動定律推導出來[1]。
在動力學裏,虛功原理會被推廣為達朗貝爾原理。這原理是拉格朗日力學的理論基礎。更詳盡細節,請參閱相關條目。
適用案例
在此特別列出幾個案例,展示出約束力所做的符合約束條件的虛功的總合是零:
- 。
- 在這裏,有兩種可能的狀況:
- 1、:
- 對於這狀況,由於,兩個作用力所做的虛功相互抵銷,也就是說,
- ,
- 所以,約束力所做的虛功的總合是零。
- 對於這狀況,由於,兩個作用力所做的虛功相互抵銷,也就是說,
- 2、 :
- 由於,
- 。
- 由於,
- 1、:
- 所以,約束力所做的虛功的總合是零。
- 所以,在剛體內,質點與質點之間的約束力所作的虛功的總合是零。
- 思考置放於平滑地面上的一塊木塊。因為木塊的重量,而產生的反作用力,是地面施加於木塊的一種約束力。注意到對於這案例,符合約束條件的虛位移必須與地面平行,所以,地面施加的約束力垂直於虛位移,它所作的虛功等於零。[3]。
參見
- 柔度法
- 拉格朗日力学
- 哈密頓力学
參考文獻
- Lanczos, Cornelius, , Dovers Publications, Inc: pp. 74–87, 1970, ISBN 978-0-486-65067-8
- Torby, Bruce, , HRW Series in Mechanical Engineering, United States of America: CBS College Publishing: pp. 263, 1984, ISBN 0-03-063366-4 (英语)
- Goldstein, Herbert. 3rd. Addison Wesley. 1980: pp. 17. ISBN 0201657023 (英语).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.