角平分线长公式

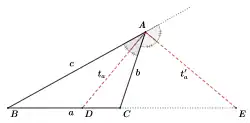
三角形的内、外角平分线

在平面几何中，角平分線長公式是計算三角形內、外角平分線長度的公式。在三角形 $\triangle {ABC}$ 中， $\angle A$ 的内角平分線交对边 $BC$ 于点 $D$ ，外角平分線交直线 $BC$ 于点 $E$ ，则三角形的内、外角平分線的长度为：

AD={\sqrt {AB\cdot AC-DB\cdot DC}}

AE={\sqrt {EB\cdot EC-AB\cdot AC}}

若记 $BC$ 边长为 $a$ ， $AC$ 边长为 $b$ ， $AB$ 边长为 $c$ ，记内角平分線 $AD$ 长为 $t_{a}$ ，外角平分線 $AE$ 长为 $t_{a}'$ ，则三角形的内、外角平分線的长度可以表示为：

t_{a}={\sqrt {bc(1-{a^{2} \over (b+c)^{2}})}}

={bc \over b+c}{\sqrt {2+2\cos A}}

={2bc \over b+c}\cdot \cos {A \over 2}

t_{a}'={\sqrt {bc({a^{2} \over (b-c)^{2}}-1)}}

={bc \over |b-c|}{\sqrt {2-2\cos A}}

={2bc \over |b-c|}\cdot \sin {A \over 2}

证明

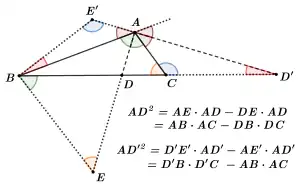
三角形ABC以及關於角A的平分線

作 $\angle A$ 的内角平分線交对边 $BC$ 于点 $D$ 。延长 ${\overline {AD}}$ 至点 $E$ ，使 $\angle AEB=\angle ACD$ 。

\triangle AEB\sim \triangle ACD\Rightarrow AE\cdot AD=AB\cdot AC

\triangle DEB\sim \triangle DCA\Rightarrow DE\cdot AD=BD\cdot DC

AD^{2}=(AE-DE)\cdot AD=AE\cdot AD-DE\cdot AD=AB\cdot AC-DB\cdot DC

得内角平分线长公式（i）：[1][2][3]

AD={\sqrt {AB\cdot AC-DB\cdot DC}}

作 $\angle A$ 的外角平分線交直线 $BC$ 于点 $D'$ 。延长 ${\overline {D'A}}$ 至点 $E'$ ，使 $\angle AE'B=\angle ACD'$ 。

\triangle AE'B\sim \triangle ACD'\Rightarrow AE'\cdot AD'=AB\cdot AC

\triangle D'E'B\sim \triangle D'CA\Rightarrow D'E'\cdot AD'=BD'\cdot D'C

AD'^{2}=(D'E'-AE')\cdot AD'=D'E'\cdot AD'-AE'\cdot AD'=D'B\cdot D'C-AB\cdot AC

得外角平分线长公式（i）：[2]

AD'={\sqrt {D'B\cdot D'C-AB\cdot AC}}

DB={ac \over b+c},\ DC={ab \over b+c}

D'B={ac \over |b-c|},\ D'C={ab \over |b-c|}

代入式（i），得到角平分线长公式（ii）：[5][3]

t_{a}={\sqrt {bc(1-{a^{2} \over (b+c)^{2}})}}

t_{a}'={\sqrt {bc({a^{2} \over (b-c)^{2}}-1)}}

将余弦公式代入式（ii），得到角平分线长公式（iii）：

t_{a}={bc \over b+c}{\sqrt {2+2\cos A}}

t_{a}'={bc \over |b-c|}{\sqrt {2-2\cos A}}

将半角公式代入式（iii），得到角平分线长公式（iv）：[6]

t_{a}={2bc \over b+c}\cdot \cos {A \over 2}

t_{a}'={2bc \over |b-c|}\cdot \sin {A \over 2}

角平分线长公式是斯图尔特定理的特殊情况，或者说推论。根据斯图尔特定理，对于三角形 $\triangle {ABC}$ 的任意一边 $BC$ 上的任意一点 $D$ ，有：

AD^{2}=AB^{2}\cdot {DC \over BC}+AC^{2}\cdot {DB \over BC}-DB\cdot DC

当点 $D$ 是内角平分线足时，根据角平分线定理，有：

{AB \over DB}={AC \over DC}={AB+AC \over BC}

联立之后，即可得到内角平分线长公式（i）或（ii）。同理，可以推出外角平分线长公式（i）或（ii）。[5][2]

利用角平分線長公式，可以证明施泰纳-莱穆斯定理——有两条内角平分线长度相等的三角形是等腰三角形。[7]

t_{a}=t_{b}\ \,\Rightarrow \ \,{\sqrt {bc(1-{a^{2} \over (b+c)^{2}})}}={\sqrt {ac(1-{b^{2} \over (a+c)^{2}})}}

化简后得到： $c(a+b+c)(a-b)[(a+b)(c^{2}+ab)+3abc+c^{3}]=0$

连乘的其他各项都为正数，从而推出： $a-b=0$

在欧美，角平分線長公式没有特殊的名称。[5][2][7]在中国大陆，内角平分線長公式（i）被称为“斯库顿定理”，归功于荷兰数学家弗兰斯·范斯霍滕。[1][8][9]而在欧美，范斯霍滕定理指的是等边三角形外接圆的一个性质，与三角形角平分线无关。[10]

孙建斌. . 数学教学研究. 1986, (1): 3-6.
别列标尔金. . 马忠林 (译). 北京: 高等教育出版社. 1955: 202-204.
Amarasinghe, G. W. I. S. (PDF). Global Journal of Advanced Research on Classical and Modern Geometries. 2012, 1 (1): 15-27 [2023-06-24]. （原始内容存档 (PDF)于2022-06-18）（英语）.
Heath, Thomas L. (PDF) II. Cambridge: Cambridge University Press. 1908: 197 [2023-06-24]. （原始内容存档 (PDF)于2022-02-02）（英语）.
Hadamard, Jacques. . Paris: Armand Colin et Cie. 1898: 122-125 （法语）.
. mathvox.com. [2023-06-24]. （原始内容存档于2023-06-17）（英语）.
Trigg, Charles W. . New York: Dover Publications. 1985: 103 [1967]. ISBN 0-486-24949-2 （英语）.
刘运谊. . 数学教学通讯. 1994, (6): 12+39.
黄家礼. . 北京: 科学普及出版社. 1997: 78. ISBN 7-110-03511-5.
Raymond, Viglione. . Mathematics Magazine. 2016, 89 (2): 132 （英语）.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.