費雪法 (統計學)
費雪法(英語:),或稱費雪合併機率檢驗(英語:)是統計學中用於合併多個p值的方法,[1][2]由羅納德·愛爾默·費雪所創,常應用於元分析。其基本形式是結合源於同一個虛無假設(H0)之下多個獨立性檢驗的結果。
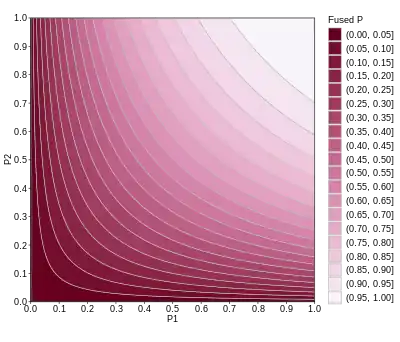
應用
費雪法用於結合各個檢驗的極端值機率(即p值)成一個卡方統計量:
- ,
其中pi為第i個檢驗之p值。當pi較小則卡方統計量X2較大而拒絕整體虛無假說。
若所有的虛無假說皆為真,且pi(或各統計檢驗量)皆相互獨立,則X2服從自由度為2k的卡方分布,其中k表示所有參與的假說檢定個數。按此可以取得聯合檢驗之p值,即對多個p值進行合併。
此卡方統計量的分布服從卡方分布的原因是:對於每一個統計檢驗i,其p值(pi)服從界於0至1的均勻分布。均勻分布取自然對數的相反數又服從指數分布。指數分布乘2又服從自由度為2的卡方分布。最終,k項獨立的卡方統計量(每項自由度為2)之總和服從自由度為2k的卡方分布。
獨立性前提的限制
當各檢驗不獨立時,X2偏大、整體p值偏小使推論過份偏好對立假說。因此,在不獨立的統計檢驗量間使用費雪法時,若整體p值較大較無所謂;但若整體p值很小則可能發生型一錯誤。
獨立性前提的擴展
在統計檢驗不相互獨立時,X2的虛無分布並不單純。常見的策略是採用縮放過的卡方隨機變數近似虛無分布。若已知p值間的共變異數,亦存在其它近似方法。
以布朗法為例,[3]該方法可用於結合二個相依p值,當其統計檢定量為共變異數矩陣已知的多元常態分布。此外,科斯特法擴大了布朗法的條件:共變異數矩陣由已知擴展至未知但具純量乘法常數即可。[4]
結果解讀
費雪法通常用於一系列相互獨立的統計檢驗,例如是具有相同虛無假說的各別研究。這與元分析的虛無假說經常是各別的虛無假說皆為真的情況相符。因此,費雪法結果若支持對立假說,則可解讀為至少存在一個對立假說為真。
在某些情況下,考慮各研究的「異質性」是有意義的,特別是某些研究支持虛無假說但某些支持對立假說,或是不同研究具有不同的對立假說。不同的對立假說形成的異質性可能是源於效果量在不同研究間不均。例如,考慮一系列針對葡萄糖攝取量對罹患第2型糖尿病的風險之研究,由於各研究間的對象存在遺傳或環境上的差異,特定葡萄糖攝取量所對應的罹患風險在各研究間亦可能不同。
在各別對立假說是全真或全偽的情況下,例如檢驗某種物理定律,單獨研究或實驗的結果若不一致則是偶然造成的,例如存在檢定力差異。
在元分析中若採用雙尾檢驗,即使部分各別研究指出存在強烈但方向不等的效果,仍可能拒絕整體虛無假設。在這種情況下,雖然可以解讀為至少存在一個研究中的虛無假說為偽,但這並不意味著應支持所有研究的對立假說。因此,雙尾元分析對對立假說中的異質性特別敏感。採用單尾檢驗的元分析可以檢測效果量的異質性,但側重於單一且預先指定的影響方向。
與斯托夫Z值法的關係
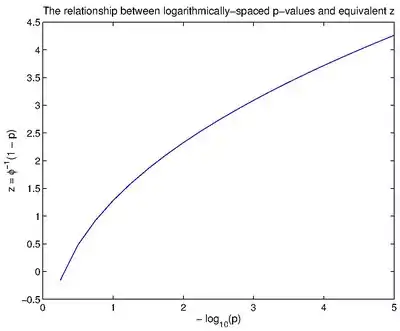
斯托夫Z值法(由社會學家山繆·安德魯·斯托福所創)與費雪法的作用相似,但前者可納入不同研究間具有不同的權重。[7][8][9]
令Zi = Φ − 1(1−pi),其中Φ為標準常態分布的累積分布函數,則
稱為元分析的整體Z值,其中w為各研究的權重。
由於費雪法基於「平均p值」而斯托夫Z值法基於「平均z值」,二者的關係遵循z與−log(p) = −log(1−Φ(z))的關係。在常態分布之下,二者並非線性關係,但z值經常存在的範圍(1至5)之內的關係較線性。因此,二種方法的檢定力通常很接近。
參考資料
- Fisher, R.A.
 . Oliver and Boyd (Edinburgh). 1925. ISBN 0-05-002170-2.
. Oliver and Boyd (Edinburgh). 1925. ISBN 0-05-002170-2. - Fisher, R.A.; Fisher, R. A. . The American Statistician. 1948, 2 (5): 30–31. JSTOR 2681650. doi:10.2307/2681650.
- Brown, M. . Biometrics. 1975, 31 (4): 987–992. JSTOR 2529826. doi:10.2307/2529826.
- Kost, J.; McDermott, M. . Statistics & Probability Letters. 2002, 60 (2): 183–190. doi:10.1016/S0167-7152(02)00310-3.
- Good, I J. . Journal of the American Statistical Association. 1958, 53 (284): 799–813. JSTOR 2281953. doi:10.1080/01621459.1958.10501480.
- Wilson, D J. . Proceedings of the National Academy of Sciences USA. 2019, 116 (4): 1195–1200. Bibcode:2019PNAS..116.1195W. PMC 6347718
 . PMID 30610179. doi:10.1073/pnas.1814092116
. PMID 30610179. doi:10.1073/pnas.1814092116  .
. - Stouffer, S.A.; Suchman, E.A.; DeVinney, L.C.; Star, S.A.; Williams, R.M. Jr. . Princeton University Press, Princeton. 1949.
- Mosteller, F.; Bush, R.R. . Lindzey, G. (编). . Addison_Wesley, Cambridge, Mass. 1954: 289–334.
- Liptak, T. . Magyar Tud. Akad. Mat. Kutato Int. Kozl. 1958, 3: 171–197.
相關條目
- 費雪法的擴展